LC Oscillations
The electric current and the charge on the capacitor in the circuit undergo electrical LC oscillations when a charged capacitor is connected to an inductor. The electrical energy stored in the capacitor is its initial charge which is named as qm. It is represented by
\({{U}_{E}}\,=\,\frac{1}{2}\frac{{{q}^{2}}_{m}}{C}\)
The inductor contains zero energy. Charge varies sinusoidal with respect to time.
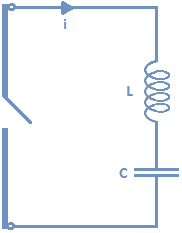
When the switch is turned on, current in the circuit starts increases and the charge on the capacitor keeps decreasing. The current induced in the circuit produces a magnetic field in the inductor. When the current increase to its maximum level Im the magnetic energy in the circuit is represented as
\({{U}_{B}}\,=\,\frac{1}{2}L_{m}^{2}\)
The magnetic field starts decreasing with time as there is no further change in current through the inductor. The current is induced in the circuit as a result of decreasing magnetic field. With reverse polarization, current starts charging the capacitor. This process is repeated again and again, once the capacitor in the circuit is fully charged with regards to its previous states. Due to this reason energy in the whole system oscillates between the capacitor and the inductor.
On applying Kirchhoff’s law to the circuit we conclude that the charge oscillates with a natural frequency.
\({{\omega }_{0}}\,=\,\frac{1}{\sqrt{LC}}\)
However, practically this whole process in not possible and is never achieved. The reason for the discrepancy is some loss of energy due to resistance in the circuit and also due to radiations in the form of electromagnetic waves.
