Let the equation of a plane be ax + by + cz + d = 0
When P and Q are on the same side of the plane
⇒ \(\frac{a{{x}_{1}}+b{{y}_{1}}+c{{z}_{1}}+d}{a{{x}_{2}}+b{{y}_{2}}+c{{z}_{2}}+d}<0\)
⇒ \(\frac{a{{x}_{1}}+b{{y}_{1}}+c{{z}_{1}}+d}{a{{x}_{2}}+b{{y}_{2}}+c{{z}_{2}}+d}>0\)
⇒ ax1 + by1 + cz1 + d and ax2 +by2 + cz2 + d are of the same sign.
When P and Q are on the opposite side of the plane
⇒ \(\frac{a{{x}_{1}}+b{{y}_{1}}+c{{z}_{1}}+d}{a{{x}_{2}}+b{{y}_{2}}+c{{z}_{2}}+d}<0\)
⇒ ax1 + by1 +cz1 + d and ax2 + by2 + cz2+ d are of opposite sign.
Perpendicular Distance of a point from a plane: The length of the perpendicular from the point P (x1, y1, z1) on the plane ax + by + cz + d = 0 is \(\frac{\left| a{{x}_{1}}+b{{y}_{1}}+c{{z}_{1}}+d \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}\).
Distance between Parallel Planes:
Let ax1 + by1 + cz1 + d = 0 … (i)
And, ax2 + by2 + cz2 + d = 0 … (ii)
Be two parallel planes
Then, the distance between them \(\frac{\left| {{d}_{1}}-{{d}_{2}} \right|}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}}}\).
Image of a Point in a Plane: Let P an Q be two points and let π be a plane such that
i) Line PQ is perpendicular to the plane π, and
ii) Mid-point of PQ lies on the plane π. Then either of the point is the image of the other in the plane π.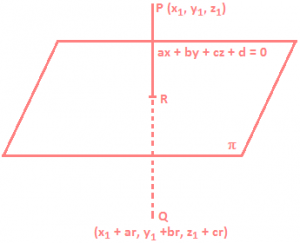
In order to find the image of a point in a given plane. We may use the following algorithm
Algorithm:
Step I: Write the equations of the line passing through P and normal – to the given plane as \(\frac{x-{{x}_{1}}}{a}=\frac{y-{{y}_{1}}}{b}=\frac{z-{{z}_{1}}}{c}\).
Step II: Write the coordinates of image Q as (x1 + ar, y1 + br, z1 + cr).
Step III: Find the coordinates of the mid-point R of PQ.
Step IV: Obtain the value of r by putting the coordinates of R in the equation of the plane.
Step V: Put the value of r in the coordinates of Q.
Example: Find the image of the point (3, -2, 1) in the plane 3x – y + 4z = 2.
Solution: Let Q be the image of the point P (3, -2, 1) in the plane 3x – y + 4z = 2. Then, PQ is normal to the plane.
Therefore, direction ratios of PQ are 3, -1, 4. Since PQ passes through P (3, -2, 1) and has direction ratios 3, -1, 4.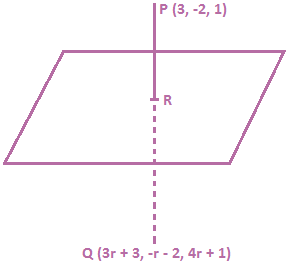
Therefore, its equations is \(\frac{x-3}{3}=\frac{y+2}{-1}=\frac{z-1}{4}=r\).