Let θ be the angle between two straight lines AB and AC whose direction cosines are given by l₁, m₁, n₁ and l₂, m₂, n₂ respectively. Then the angle between the lines AB and AC is given by cos θ = l₁ l₂ + m₁ m₂ + n₁ n₂.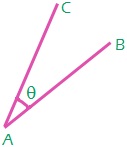
If the direction ratios of the two lines are a₁, b₁, c₁ and a₂, b₂, c₂, then the angle between the two lines is given by \(\cos \theta \,=\,\frac{\left( {{a}_{1}}{{a}_{2}}\,+\,{{b}_{2}}{{b}_{1}}\,+\,{{c}_{1}}{{c}_{2}} \right)}{\sqrt{\left( a_{1}^{2}\,+\,b_{1}^{2}\,+\,c_{1}^{2} \right)}.\sqrt{\left( a_{2}^{2}\,+\,b_{2}^{2}\,+\,c_{2}^{2} \right)}}\).
The lines can either be parallel, coplanar or perpendicular. Whether they are parallel, coplanar or perpendicular can be decided with the help of their direction cosines
Problem: The acute angle between the two lines whose direction ratios are given by l + m – n = 0 and l² + m² – n² = 0.
Solution: n = l + m substituting in l² + m² = n² ⇒ lm = 0
if l = 0 ⇒ m = n ⇒ \(\frac{l}{0}=\frac{m}{1}=\frac{n}{1}\),
m = 0 ⇒ l = n ⇒ \(\frac{l}{1}\,=\,\frac{m}{0}\,=\,\frac{n}{1}\),
\(\cos \theta \,=\,\frac{\left( {{a}_{1}}{{a}_{2}}\,+\,{{b}_{2}}{{b}_{1}}\,+\,{{c}_{1}}{{c}_{2}} \right)}{\sqrt{\left( a_{1}^{2}\,+\,b_{1}^{2}\,+\,c_{1}^{2} \right)}.\sqrt{\left( a_{2}^{2}\,+\,b_{2}^{2}\,+\,c_{2}^{2} \right)}}\),
\(\cos \theta \,=\,\frac{\left( 0+\text{ 0}+\text{ 1} \right)}{\sqrt{\left( 2 \right)}.\sqrt{\left( 2 \right)}}\,=\,\frac{1}{2}\),
\(\theta \,=\,\frac{\pi }{3}\).