Heights and Distances – Problems
1. The upper ¾ th portion of a vertical pole subtends an angle θ such that tanθ = ⅗ at a point in the horizontal plane through its foot and at distance 40m from the foot. Find the possible height of the vertical pole.
Solution: Let h be the height of the pole
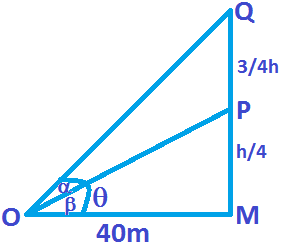
The position PQ subtend an angle β at O such that
Tanβ = 3/5
θ = α + β
β = θ – α
\(\tan \beta =\frac{\tan \theta -\tan \alpha }{1+\tan \theta .\tan \alpha }\).
\(\frac{3}{5}=\frac{\frac{h}{40}\frac{h/4}{40}}{1+\frac{h}{40}.\frac{h/4}{40}}\).
\(\frac{3}{5}=\frac{\frac{h}{40}-\frac{h}{160}}{1+\frac{{{h}^{2}}}{40\times 160}}\).
\(\frac{3}{5}=\frac{3h}{160}\times \frac{40\times 160}{40\times 160+{{h}^{2}}}\).
\(\frac{1}{5}=\frac{40h}{6400+{{h}^{2}}}\).
h² – 200h + 6400 = 0
(h – 40) (h – 160) = 0
h = 40, 160
Hence h = 40m
2. The length of the shadow of a vertical pole of height h, thrown by the sun’s rays at three different moments are h, 2h and 3h. Find the sum of the angle of elevation of the rays at these moments.
Solution: Clearly tan α = h/h
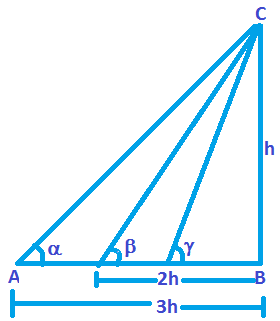
Tan α = 1
α = tan⁻¹ (1)
α = tan⁻¹ (tan 45°)
α = π/4
\(\tan \beta =\frac{h}{2h}=\frac{1}{2}\).
\(\tan \gamma =\frac{h}{3h}=\frac{1}{4}\).
\(\tan (\alpha +\beta +\gamma )=\frac{\tan \alpha +\tan \beta +\tan \gamma -\tan \alpha \tan \beta \tan \gamma }{1-\tan \alpha \tan \beta -\tan \beta \tan \gamma -\tan \gamma \tan \alpha }\).
\(=\frac{1+\frac{1}{2}+\frac{1}{3}-1.\frac{1}{2}.\frac{1}{3}}{1-\,\frac{1}{2}-\frac{1}{3}-\frac{1}{6}}\).
\(=\frac{1+\frac{4}{6}}{1-1}\).
= ∞
tan (α + β + γ) = ∞
α + β + γ = tan⁻¹ ∞
α + β + γ = π/2.
