Velocity of Transverse Wave
In a transverse wave the particle displacement is perpendicular to the direction of wave propagation. The velocity of a transverse wave in a stretched string is: \(v=\sqrt{\frac{T}{m}}\).
Where, T = Tension in the string, m = Linear density of string.
1) If A is the area of cross section of the wire then, mass (m) = ρA.
\(v=\sqrt{\frac{T}{\rho A}}=\sqrt{\frac{S}{\rho }}\); Where, S = Stress = T/ A.
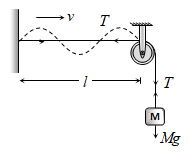
2) If string is stretched by some weight then, T = Mg ⇒ \(v=\sqrt{\frac{Mg}{m}}\),
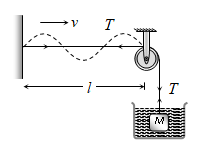
3) If suspended weight is immersed in a liquid of density σ and ρ = density of material of the suspended load then: \(T=Mg\left( 1-\frac{\sigma }{\rho } \right)\Rightarrow v=\sqrt{\frac{Mg\left( 1-\frac{\sigma }{\rho } \right)}{m}}\).
4) If two rigid supports of stretched string are maintained at temperature difference of Δθ then due to elasticity of string: T = Y A α Δθ ⇒ \(v=\sqrt{\frac{Y\,A\,\alpha \,\Delta \theta }{m}}=\sqrt{\frac{Y\,\alpha \,\Delta \theta }{d}}\).

Where, Y = Young’s modulus of elasticity of string, A = Area of cross section of string, α = Temperature of coefficient of thermal expansion, d = Density of wire = m/ A.
5) In a solid body: \(v=\sqrt{\frac{\eta }{\rho }}\),
Where, η = Modulus of rigidity; ρ = Density of the material.
