If a liquid is filled in a vessel up to height H and a hole is made at a depth h below the free surface of the liquid as shown in figure, then taking the level of hole as reference level (i.e., zero point of potential energy) and applying Bernoulli’s principle to the liquid just inside and outside the hole (assuming the liquid to be at rest inside) we get
(p₀ + hρg) + 0 = p₀ + ½ ρv²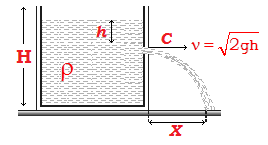 Or v = √2gh
Or v = √2gh
Which is the same speed that an object would acquire in falling from rest through a distance h and is called ‘velocity of efflux’ or velocity of flux? From this expression it is clear that:
(1) The speed of the liquid coming out of the orifice is independent of the nature and quantity of liquid in the container or the area of the orifice.
(2) Greater is the distance of the hole from the free surface of liquid greater will be the velocity of efflux (i.e.). This is why liquid gush-out with maximum velocity from the orifice which is at maximum vertical distance from the free surface of the liquid.
(3) As the vertical velocity of liquid at the orifice is zero and it is at a height (H – h) from the base, the time taken by the liquid to reach the base-level t = √2(H – h)/g
Now during this time liquid is moving horizontally with constant velocity v, so it will hit the base.
Level at a horizontal distance x (called range) as shown in figure such that
x = vt = √2gh x √2(H – h)/g = 2 √h(H – h)
From this expression it is clear that x will be maximum when x² is maximum
i.e., \(\frac{d}{dh}({{x}^{2}})=0\) or \(4\frac{d}{dh}(Hh-{{h}^{2}})=0\) or H – 2h = 0 i.e., h = H/2
So that \({{x}_{\max }}=2\sqrt{\frac{H}{2}\left[ H-\frac{H}{2} \right]}=H\)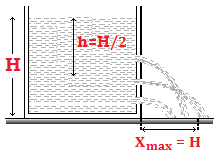 i.e., range x will be maximum (=H) when h = H/2.
i.e., range x will be maximum (=H) when h = H/2.
