Phase relationship between displacement, velocity and acceleration of SHM
As we have seen that
x = A sin (ωt + φ)
v = A ω cos (ωt+ φ)
= Aω sin (ωt + φ + π/2)
And a= – Aω2 sin (ωt + φ)
= Aω2 sin (ω t + φ + π)
Thus, we conclude that in SHM, particle velocity is ahead in phase by π/2 as compared to the displacement and acceleration is further ahead in phase by π/2.
In figure, x, v and a as functions of time are illustrated.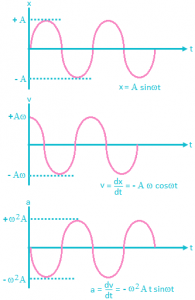
Example: The equation of motion of a particle is given by dp/ dx + mω2n = 0, where p is the momentum and n is the position. Then, the particle
1. Moves along a straight line
2. Moves along a parabola
3. Execute simple harmonic motion
4. Falls freely under gravity
Solution: dp/dt = – mω2n
dp/dt = rate of change of momentum
= F (force)
∴ F = – mω2n
m and ω are constants
∴ F α – n
Force α displacement
So, this is the condition for simple harmonic motion, so the particle will execute simple harmonic motion.
Example: A particle executing simple harmonic motion has an amplitude of 6 cm. Its acceleration at a distance from the mean position 2 cm is 8 cm s-2. The maximum speed of the particle
Solution: Amplitude, a = 6 cm
Displacement, y = 2 cm
Acceleration, A = 8 cm, s-2
A = ω2y
ω = 2 rads-1
Maximum speed, Vmax = aω = 6 x 2
= 12 cm s-1