Trigonometric Ratios, Domains and Range

Angle: Consider a ray. If this ray rotates about its end point O and takes the position OB, then we say the angle has been generated.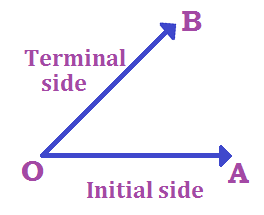Angle is considered as the figure obtained by rotating a given ray about its end point. Measure of an angle is the amount of rotation from initial side to terminal side.

System of measurements of angles:

i) Sexagesimal or English System

ii) Centesimal or French System

iii) Circular System

i) Sexagesimal System: In this system right angle is divided into 90 equal parts, called degrees.

1 right angle = 90 degrees = (90⁰)

1⁰= 60 minutes = (60¹)

1’ = 60 seconds = (60¹¹)

ii) Centismal System: In this system right angle is divided into 100 equal parts, called grades.

1 right angle = 100 degrees = (100⁰)

1 grade= 100 minutes = (100¹)

1 minute = 100 seconds = (100¹¹)

iii) Circular System: In this system unit of measurement is radian.

Radian: 1 radian = 1^c is measure of an angle subtended at the earth of a circle by an arc of length equal to the radius of circle.

Relation:

D/90 = G/100 = 2R/π

D = number of degrees

G = Number of grades

R = number of radians

Trigonometric ratios, domains and range: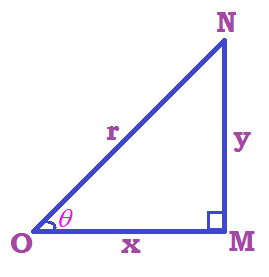Base = OM = x

Perpendicular = NM = y

Hypotenuse = ON = r

Sin θ = perpendicular/hypotenuse = y/r = sin θ

Cos θ = base/hypotenuse = x/r = cosine θ

Tan θ = perpendicular/base = y/x = tangent θ

Cot θ = base/perpendicular = x/y = cotangent θ

Sec ant θ = hypotenuse/ base = r/x = sec θ

Cosec ant θ = hypotenuse / perpendicular = r/y = cosec θ

From above definitions:

i) Sin θ x cosec θ = 1

ii) Cos θ x sec θ = 1

iii) Tan θ x cot θ = 1

iv) Tan θ = sin θ / cosθ, cotθ = cosθ / sinθ

Domain: Domain of a trigonometric ratio is the set of all values of angle θ for which it is meaningful and the range is the set of all values of trigonometric ratio for different values of θ for which it is meaningful.

Trignometric Ratio	Domain	Range
Sin θ	R	[-1,1]
Cos θ	R	[-1,1]
Tan θ	R – {(2n + 1)π/2; n ϵ Z}	R
Cot θ	R – {nπ; n ϵ Z}	R
Sec θ	R – {(2n + 1)π/2; n ϵ Z}	R – (-1,1)
Cosec θ	R – {nπ; n ϵ Z}	R – (-1,1)