Let O be the origin and let X’OX and Y’OY be the axis of x and y respectively. Let O’ and P be two points in the plane having coordinates (h, k) and (x, y) respectively referred to X’OX and Y’OY as the coordinate axes. Let the origin be transferred to O’ and let X’OX’ and Y’OY be new rectangular axes. Let the coordinates of P referred to new axes as the coordinates axes be (X, Y). Then,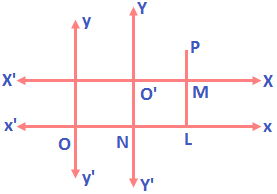 O’ N = X, PN = Y, OM = x, PM = y, OL = h and O’L = k.
O’ N = X, PN = Y, OM = x, PM = y, OL = h and O’L = k.
Now, x = OM = OL + OM = 0L + O’N = h + X
And, y = PM = PN + NM = PN + O’L = Y + k
x = X + h and y = Y + k.
Thus, if (x, y) are coordinates of a point referred to old axes and (X, Y) are the coordinates of the same point referred to new axes. Then, x = X + h and y = Y + k
Therefore, if the origin is shifted at a point (h, k) we must substitute X + h and Y + k for x and y respectively.
The transformation formula from new axes to old axes is X = x – h, Y = y – k
The coordinates of the old origin referred to the new axes are (-h, -k).
Rotation of Axes: Let ox and oy be the old axes and OX and OY be the new axes obtained by rotating ox and oy respectively through an angle θ. Let (x, y) be the coordinates referred to the new axes.
Draw PL and PM perpendiculars to ox and OX, and also MN and MQ perpendicular to ox and PL.
We have, OL = x, LP = y, OM = X, MP = Y
Now, x = ON – NL
= OM cos θ – PM sin θ
And, y = PL = PQ + QL
= PQ + MN
= PM Cosθ + ON sinθ
= Y cosθ + sinθ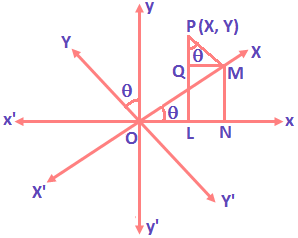 Thus, if the axes are rotated through an angle θ, then
Thus, if the axes are rotated through an angle θ, then
x = X cosθ – Y sinθ … (i)
y = X sinθ + Y cosθ … (ii)
If therefore in any equation we wish to turn the axes through an angle θ, we must substitute X cosθ – Y Sinθ and X sinθ + Y cosθ for x and y respectively.
Solving (i) and (ii) for X and Y, we get
X = x cosθ + y sinθ, Y = y cosθ + x sinθ
If the origin is shifted at O’ (h, k) and the axes are rotated about the new origin O’ by an angle θ in anticlockwise sense, then
x = h + X cosθ – Y sinθ
And, y = k + X sinθ + Y cosθ.
Example: Shift the origin to a suitable point so that the equation y2 + 4y + 8x – 2 = 0 will not contain term in y and the constant term.
Solution: Let the origin be shifted to (h, k). Then, x = X + h and y = Y + k.
Substituting x = X + h, y = Y + k in the equation
y2 + 4y + 8x – 2 = 0, we get
(Y + k) 2 + 4 (Y + k) + 8 (X + h) – 2 = 0
Y2 + (4 + 2k) Y + 8X + (k2 + 4k + 8h – 2) = 0
For this equation to be free from the term containing Y and the constant term, we must have
4 + 2k = 0 and k2 + 4k + 8h – 2 = 0
K = – 2 and h = ¾
Hence, the origin is shifted at the point (¾, – 2).
