Theory of Equations – Problems
1. Find the polynomial equation whose roots are translates of those of x⁵ – 4x⁴ + 3x² – 4x + 6 = 0 by -3.
Solution: Given equation is f(x) = x⁵ – 4x⁴ + 3x² – 4x + 6 = 0
Required equation is f(x + 3) = 0
(x + 3)⁵ – 4(x + 3)⁴ + 3(x + 3)² – 4(x + 3) + 6 = 0
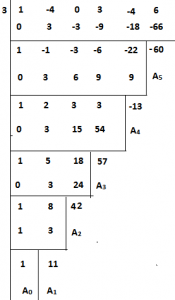
Required equation is of x⁵ + 11x⁴ + 42x³ + 57x² – 13x – 60 = 0
2. From the polynomial equation whose roots are the square of the roots of x³ + 3x² – 7x + 6 = 0
Solution: Given that x³ + 3x² – 7x + 6 = 0
Required equation is f(√x) = 0
f(√x) = (√x)³ + 3(√x)² – 7(√x) + 6 = 0
x (√x) + 3x – 7(√x) + 6 = 0
√x(x – 7) + (3x + 6) = 0
√x(x – 7) = – (3x + 6)
Squaring on both sides
x(x – 7)² = (3x + 6) ²
x (x² – 14x + 49 ) = 9x² + 36+ 36x
x³ – 23x² + 13x – 36 = 0
3. Find the algebraic equation whose roots are 3 times the roots of x³ + 2x² – 4x + 1 = 0
Solution: Given the equation is f(x) = x³ + 2x² – 4x + 1 = 0
We require an equation whose roots are 3 times the roots of f(x) = 0
Required equation is f(x/3) = 0
(x/3)³+ 2(x/3)² – 4(x/3) + 1 = 0
x³/27 + 2/9 x² – 4/3 x + 1 = 0
Multiplying with 27
Required equation is x³ + 6x² – 36x + 27 = 0
