Hydrostatic Paradox

Case i: Three vessel have different shapes, but the same base area and the same weight when empty. They are filled with water to the same level.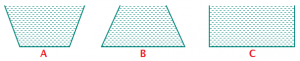a) Are the water pressure at the bottom of the each vessel are same? If not, which is larger

and which is smaller?

Solution: As, P = P_atm + P_gh

PA = PB = PC

b) If the three vessels containing water are weighed on a scale, do they give the same reading? If not, which weighs most and which weight the least?

Solution: The weight of water is more in A. Therefore, A weighs most and B weighs the least, (Assuming weight of each vessel is same).

c) Is the force excreted by the water on the base of vessel is equal to the weight of water in the vessel?

Solution: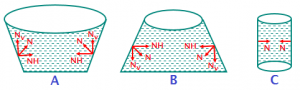From (a) we know that upward force exerted by base of each vessel is same. Let this force be F. If we draw the diagram for the liquid in each of the vessel we have: (NH and NV are horizontal and vertical components of the normal force by side walls, W is weight of fluid in vessel)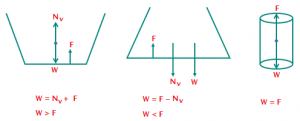Case ii: Is the pressure at point 2, P₂ is the same as the pressure at point 1, P₁ even though the column of water above point 2 is less than the column of water above point 1?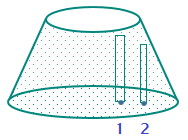Consider a horizontal cylindrical element between 1 and 2Net force acting on the cylindrical element is P₁A – P₂A = 0 as the liquid is non-acceleration.

P₁ = P₂

(i.e.) for same liquid which is not accelerating horizontally, pressure will be same at all Points which are at the same level.

Case iii: Pressure at two points at the same level of the same liquid which is not accelerating horizontally when the liquid elements at those points are in “communication” must be same. i.e.; in following situation.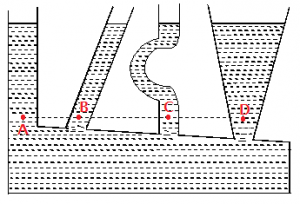Since, lengths are equal, P_A = P_B = P_C = P_D

Example: Water is filled in a flask up to a height of 20 cm. The bottom of the flask is circular with radius 10 cm. If the atmospheric pressure is 1.01 × 10⁵ Pa, find the force exerted by the water on the bottom. Take g = 10 m/s² and density of water = 1000 kg/m³.

 Solution: The pressure at the surface of the water is equal to the atmospheric pressure P0.

The pressure at the base P = P₀ + hrg

                                              = 1.01 x 10₆ Pa + (0.20m) (1000 kg/m³) (10 m/s²)

= 1.01 x 10⁵ Pa + 0.20 x 10⁵ Pa = 1.03 x 10⁵ Pa

 The area of the bottom = πr²

                                                         = 3.14 x (0.1m)

                                                         = 0.0314 m2

The force on the bottom is, therefore,

F = Pπr² = (1.03 x 10⁵) x (0.0314m²) = 3230N.