Temperature of the Sun and Solar Constant
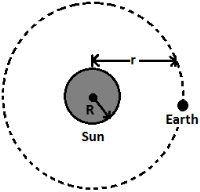
If R is the radius of the sun and T is the temperature, then the energy emitted by the sun per second through radiation in accordance with Stefan’s law be given by P = AσT⁴ = 4πR²σT⁴.
By the time it reaches the earth, this energy will spread over a sphere of radius r (= Average distance between sun and earth). So, the intensity of solar radiation at the surface of earth (called solar constant S) will be given by:
\(S=\frac{P}{4\pi {{r}^{2}}}=\frac{4\pi {{R}^{2}}\sigma {{T}^{4}}}{4\pi {{r}^{2}}}\).
i.e., \(T={{\left[ {{\left( \frac{r}{R} \right)}^{2}}\frac{S}{\sigma } \right]}^{1/4}}\).
\(T={{\left[ {{\left( \frac{1.5\times {{10}^{8}}}{7\times {{10}^{5}}} \right)}^{2}}\times \left( \frac{1.4\times {{10}^{3}}}{5.67\times {{10}^{-8}}} \right) \right]}^{1/4}}\) = 5800 K.
∴ T = 5800 K.
As r = 1.5 x 10⁸ Km, R = 7 x 10⁵ Km.
S = 2 [cal/ (cm². min)] = 1.4 (KW/ m²) and σ = 5.67 x 10⁻⁸ W/ m² K⁴.
This result is in good agreement with the experimental value of temperature of sun, i.e., 6000K.
