Intersection of straight line and a circle: Let the equation of circle be x² + y² = a² and the equation of the line be y = mx + c then
When points of intersection are real and distinct: Then length of perpendicular from centre should be less the radius.
∴ \(\left| \frac{c}{\sqrt{1+{{m}^{2}}}} \right|<a\).
When points of intersection are coincident: Line touches the circle if the length perpendicular from centre is equal to radius.
∴ \(\left| \frac{c}{\sqrt{1+{{m}^{2}}}} \right|=a\).
When points of intersection are imaginary: Line does not intersect a circle if the length of perpendicular from centre is greater than radius of circle.
∴ \(\left| \frac{c}{\sqrt{1+{{m}^{2}}}} \right|>a\).
Length of the intercept cut off from the line y = mx + c by the circle x² + y² = a² is \(2\sqrt{\frac{{{a}^{2}}\left( 1+{{m}^{2}} \right)-{{c}^{2}}}{1+{{m}^{2}}}}\).
Condition of Tangency: The line y = mx + c touches the circle x² + y² = a² if the length of the intercepts is zero i.e., c = ± a √(1 + m²).
Tangent to a circle: Let P be a point on circle and let PQ be secant.
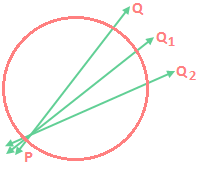
Tangent at point P is the limiting position of a secant PQ when Q tends to P along the circle. The point P is called the point of contact of the tangent.
Different forms of equation of tangents:
⇒ The equation of tangent of slope m to the circle x² + y² = a² is y = mx ± a √(1 + m²) the coordinates of the point of contact are \(\left( \pm \frac{am}{\sqrt{1+{{m}^{2}}}},\,\,\mp \frac{a}{\sqrt{1+{{m}^{2}}}} \right)\).
⇒ The equations of tangents of slope m to the circle (x – a)² + (y – b)² = r² are given by y – b = m (x – a) ± r √(1 + m²) and the coordinates of point of contact are \(\left( a\pm \frac{mr}{\sqrt{1+{{m}^{2}}}},\,\,b\mp \frac{r}{\sqrt{1+{{m}^{2}}}} \right)\).
⇒ The equations of the tangents of slope m to circle x² + y² + 2gx + 2fy + c = 0 is y + f = m(x + g) ± \(\sqrt{\left( {{g}^{2}}+{{f}^{2}}-c \right)\left( 1+{{m}^{2}} \right)}\).
Point form: The equation of the tangent at the point P(x₁, y₁) to a circle x² + y² + 2gx + 2fy + c = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0.
Parametric form: The equation of the tangent to the circle x² + y² = a² at the point (a cosθ, a sinθ) is x cosθ + y sinθ = a.
The equation of tangent to the circle (x – a)² + (y – b)² = r² at the point (a + r cosθ, b + r sinθ) is (x – a) cosθ + (y – b) sinθ = r.
