System of Planes
An equation of the plane contains three independent constants as such a plane is uniquely determined by three independent conditions. If we consider a plane satisfy just two given conditions, its equation will contain one arbitrary constant. If we consider a plane satisfy one condition.it equations contain two arbitrary constants
We have given some well-known equations of System of Plane below:
(i) The equation ax + by + cz + k = 0 represent a system of the plane parallel to the plane ax + by + cz + d = 0, where k is parameter.
(ii) The equation ax + by + cz + k = 0 represent a system of plane perpendicular to the line \(\frac{x}{a}=\frac{y}{b}=\frac{z}{c}\).
(iii) The equation (a₁x + b₁y + c₁z + d₁) + k (a₂x + b₂y + c₂z + d₂) = 0
Represent a system, of planes passing through the intersection of plans a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0, where k is parameter
(iv) The equation A (x – x₁) + B (y – y₁) + C (z – z₁) = 0
Represent a system of plane passing through the point (x₁, y₁, z₁), the ratios of A, B, C being the two parameters
It may be noted that (i) to (iii) above are examples of one parameter family of planes and (iv) is an example of two parameter family of planes.
Parallelism and perpendicularity of two planes: The planes a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0 are parallel if and only if \(\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{{{c}_{1}}}{{{c}_{2}}}\) and perpendicular if and only if a₁a₂ + b₁b₂ + c₁c₂ = 0.
Two sides of a plane: Two points P (x₁, y₁, z₁) and Q (x₂, y₂, z₂) lie on the same and different sides of plane ax + by + cz + d = 0 according as a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0 are of the same or of different signs.
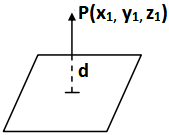
Length of the perpendicular from a point to the plane: The perpendicular distance of the point (x₁, y₁, z₁) from the plane lx + my + nz = p is |p – lx₁ – my₁ – nz₁|.
Where l, m, n are direct cosines of the normal to the plane and p is the length of the perpendicular to the plane from the origin.
The perpendicular distance of the point (x₁, y₁, z₁) from the plane ax + by + cz + d = 0 is
\(d=\frac{\left| a{{x}_{1}}+b{{y}_{1}}+c{{z}_{1}}+d \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}\)
Example: The plane through the point A, B, C whose coordinates are (1, 1, 1), (1, -1, 1) and (-1, 3, -5) passing through the point (2, k, 4) for all values of k.
Solution: Let the equation of the plane passing through A (1, 1, 1)
be a (x – 1) + b (y – 1) + c (z – 1) = 0 …. (1)
Since (1) passing through the of the B (1, -1, 1)
-2b = 0
∴ b = 0
∵ Equation (1) passing through the of the C (-1, 3, -5)
-2a – 4b – 6c = 0 … (2)
(∵ b = 0)
-2a – 6c = 0
a + 3c = 0
a = – 3c
a/c = -3/1
∴ a = – 3 and c = 1
The equation of the becomes
-3 (x – 1) + z – 1 = 0
-3x + 3 + z – 1 = 0
3x – z – 2 = 0
Which passing through (2, k, 4) for all values of k.
