Sticking of a Person with the Wall of Rotor
A person with a mass m stands in contact against the wall of a cylindrical drum (rotor). The coefficient of friction between the wall and the clothing is \(\mu \). If rotor starts rotating about its axis, then person thrown away from the center due to centrifugal force at a particular speed \(\omega \), the person stuck to the wall even the floor is removed, because friction force balances its weight in this condition.
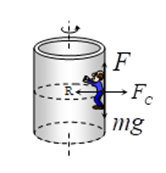
From the figure, we can write:
Frictional Force\(\left( {{F}_{f}} \right)=\) Weight of person \(\left( mg \right)\)
Frictional force is the force generated by two surfaces that contact and slide against each other and these forces are mainly affected by the surface texture and amount of force impelling them together.
\(\Rightarrow \mu R=mg\),
\(\Rightarrow \mu {{F}_{C}}=mg\),
Where, \({{F}_{C}}=\) Centrifugal Force
If an object moving in a circle and experiences an outward force, then this force is called as centrifugal force.
\(\Rightarrow \mu m\omega _{\min }^{2}R=mg\),
\(\Rightarrow {{\omega }_{\min }}=\sqrt{\frac{g}{\mu R}}\)Where, g = Acceleration due to gravity.
