Let S be the focus, ZK the directrix and e the eccentricity of the ellipse whose equation is required. Draw SK perpendicular from S on the directrix. Divide SK internally and externally at A and A’ (on SK produced) respectively in the ratio e : 1.
∴ \(\frac{SA}{KA}=\frac{e}{1}\) ⇒ SA = e. AK … (1)
And
\(\frac{SA’}{A’K}=\frac{e}{1}\) ⇒ SA’ = e A’K … (2)
Since A and A’ are such points that their distances from the focus bear constant ratio e (< 1) to their respective distances from the directrix. Therefore these points lie on the ellipse.
Let AA’ = 2a and C be the mid – point of AA’. Then CA = CA’ = a
Adding (i) and (ii), we get
SA + SA’ = e (AK + A’K)
⇒ 2a = e (CK – CA + A’C + CK)
⇒ 2a = 2e CK [∵ CA = A’C = a]
⇒ CK = a/e … (3)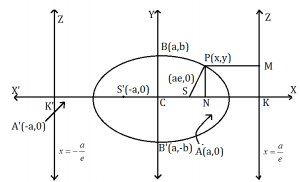
Subtracting (i) from (ii), we get
SA’ – SA = e (A’K – AK)
⇒ (SC + CA’) – (CA – CS) = e (AA’)
⇒ 2CS = 2ae
⇒ CS = ae
Now let us choose C as the origin. CAX as x-axis and a line are (ae, 0) and equation of the directrix ZK is z = a/e.
Let P(x, y) be any point on the ellipse. Join SP and draw PM ZK. Then, by definition, we have
SP = e PM
⇒ SP² = e² PM²
⇒ (x – ae)² + (y – 0)² = e² (a/e – x)²
⇒ x² (1 – e²) + y² = a² (1 – e²)
⇒ \(\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{a}^{2}}\left( 1-{{e}^{2}} \right)}=1\)
⇒\(\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\), Where b² = a² (1 – e²)
This is the standard equation of the ellipse.
Note:
e < 1 ⇒ 1 – e² < 1 ⇒ a² (1 – e²) < a² ⇒ b² = a².
Tracing of the ellipse \(\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\), when a > b
We have,
\(\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\), where a > b … (1)
∴ \(y=\pm \frac{b}{a}\sqrt{{{a}^{2}}-{{x}^{2}}}\) … (2)
And \(x=\pm \frac{a}{b}\sqrt{{{b}^{2}}-{{y}^{2}}}\)… (3)
We observe the following:
Symmetry: For every value of x there are equal and opposite values of y. Similarly for every value of y there are equal and opposite values of x.
Thus, the curve is symmetric about both the axes.
Origin: The curve does not pass through the origin.
Intersection with axes: The curve meets x axis at y = 0
Putting y = 0 (iii), we get x = ± a.
So the curve meets y-axis at A (a, 0) and A’ (-a, 0).
Putting x = 0 in (ii), we get y = ± b.
So the curve meets y-axis at B (0, b) and B’ (0, -b).
Region: if x > a or, x < -a, from (ii) we get imaginary values of y, therefore, there is no part of the curve to the right of A or to the left of A’
If y > b or y < -b, from (iii) we get imaginary values of x. therefore, there is no part of the curve above B (0, b) or below B’ (0, -b).
From (ii), we find that at x = 0, y = ±b and as x increases the convenient points on the ellipse the general shape of the ellipse \(\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\).