Square Roots of a Complex Number: Let a + ib be a complex number such that √(a + ib) = x + iy, where x and y are real numbers.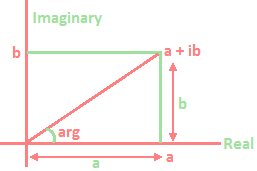
If b is positive \(\sqrt{a+ib}=\pm \left\{ \sqrt{\frac{1}{2}\left\{ \sqrt{{{a}^{2}}+{{b}^{2}}}+a \right\}+i\left\{ \sqrt{{{a}^{2}}+{{b}^{2}}}-a \right\}} \right\}\).
If b is negative \(\sqrt{a+ib}=\pm \left\{ \sqrt{\frac{1}{2}\left\{ \sqrt{{{a}^{2}}+{{b}^{2}}}+a \right\}-i\left\{ \sqrt{{{a}^{2}}+{{b}^{2}}}-a \right\}} \right\}\).
Geometrical representation of Conjugate of a Complex Number: Let z = x + iy be a complex number. Clearly z = x + iy is represented by a point P (x, y) in the argand plane.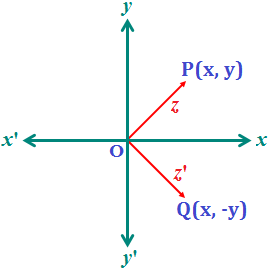
Now, z = x + iy ⇒ z̄ = x – iy = x – iy = x + (-y). So, z̄ is represented by a point Q (x, -y) in the argand plane.
Clearly, Q is the image of point P in the real axis.
Thus, if a point P represents a complex number z, then its conjugate z̄ is represented by the image of P in the real axis.
|z| = |z̄| and arg (z̄) = -arg (z).
The general value of arg (z̄) is 2nπ + arg (z).