When a body repeats its motion after regular time intervals we say that it is in harmonic motion or periodic motion. The time interval after which the motion is repeated is called the time period. If a body moves to and fro on the same path, it is said to perform oscillations. Simple harmonic motion (SHIA) is a special type of oscillation in which the particle oscillates on a straight line, the acceleration of the particle is always directed towards a fixed point on the line and its magnitude is proportional to the displacement of the particle from this point. This fixed point is called the centre of oscillation. Taking this point as the origin and the line of motion as the X-axis, we can write the defining equation of a simple harmonic motion as
a = ω² x
Time Period of Pendulum:
A simple pendulum is defined as an object that has a small mass, also known as the pendulum bob, which is suspended from a wire or string of negligible mass. When displaced, a pendulum will oscillate around its equilibrium point due to momentum in balance with the restoring force of gravity.
There are only two forces acting on the bob; the tension T along the string and the vertical force due to gravity. The force mg can be resolved into the component along the string and perpendicular to it. Since the motion of the bob is along a circle of radius and centre at the support point, the bob has a radial acceleration and also a tangential acceleration; the latter arises since motion along the arc of the circle is not uniform. The radial acceleration is provided by the net radial force, while the tangential acceleration is provided by mg sinθ.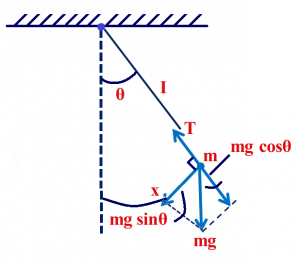 According to Newton’s 2nd law
According to Newton’s 2nd law
mg sinθ = ma
Here mg sinθ acts as the centripetal Force.
a = g sinθ
When θ is small sinθ ≈ θ
a= g θ
arc length = θ * l
a = g x/l … (1)
When the body is said to be performing SHM we know that, the acceleration of the particle is always directed towards a fixed point and it is proportional to the displacement, so we can write
a = ω² x … (2)
As the bob is also performing the SHM motion we can equate both the equations (1) and (2)
By equating we get
ω² x = g x/l
ω = √ (g/l)
2π/T = √ (g/l)
T = 2π √ (g/l)
We already know that frequency f = 1/T
So frequency of Oscillations is f = 1/2π √ (g/l)
Oscillations in the spring:
Here a block of mass m connected to an elastic spring of spring constant K oscillates vertically. If the blocks is pushed down a little and released, its angular frequency of oscillation is ω = √ (k/m).
However, in practice, the surrounding medium (air) will exert a damping force on the motion of the block and the mechanical energy of the block-spring system will decrease. The energy loss will appear as heat of the surrounding medium. The damping force depends on the nature of the surrounding medium. If the block is immersed in a liquid, the magnitude of damping will be much greater and the rate of dissipation of energy much faster. The damping force is generally proportional to velocity of the bob.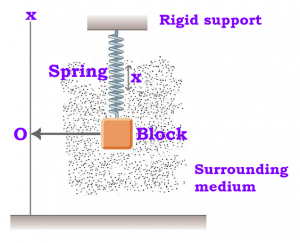 The viscous surrounding medium exerts a damping force on an oscillating spring, eventually bringing it to rest.
The viscous surrounding medium exerts a damping force on an oscillating spring, eventually bringing it to rest.
Time period of oscillations in the string
When the string is stretched by the length “x” then the restoring force in the stretched string is
F = kx
This force is responsible for the oscillations in the stretched string, now by using the Newton law
F = ma,
Where, m = mass of the block
We can write
kx = ma
a = kx / m … (1)
When the body is said to be performing SHM we know that, the acceleration of the particle is always directed towards a fixed point and it is proportional to the displacement, so we can write
a = ω²x … (2)
As the stretched string is also performing the SHM motion we can equate both the equations (1) and (2)
By equating we get
ω²x = kx /m
2π/T = √ (k/m)
T = 2π √ (k/m)
We already know that frequency f = 1/T
So frequency of Oscillations is f = 1/2π √ (m/k).
