The applied voltage V divides into three parts, VL (across L), VC (across C) and VR (across R) such that
We know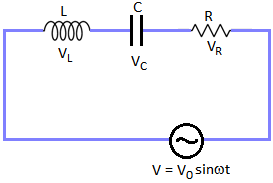 By KVL, V = VR + j (VL – VC)
By KVL, V = VR + j (VL – VC)
V = √ (V²R + (VL – VC)²)
VL Voltage across Inductor
VR Voltage across Resistor
VC Voltage across Capacitor
The impedance of the circuit is
VR = IR; VC =\(\frac{1}{\omega C}\); VL = IωL;
V = IZ
\(IZ=\sqrt{{{\left( IR \right)}^{2}}+{{I}^{2}}{{\left( \omega L-\frac{1}{\omega C} \right)}^{2}}}\).
\(Z=\sqrt{{{R}^{2}}+{{\left( \omega L-\frac{1}{\omega C} \right)}^{2}}}\).
But at some particular frequency both Inductive effect and Capacitor effect cancels each other and the circuit start oscillating. This is called resonance and the resonating frequency is
\(\omega L=\frac{1}{\omega C}\).
\({{\omega }^{2}}=\frac{1}{LC}~\).
\(\omega =\frac{1}{\sqrt{LC}}\Rightarrow f=\frac{i}{2\pi \sqrt{LC}}~\).
At this frequency the current in the circuit is maximum as impedance (Z) is minimum.
