Segments of Secants, Chord and Tangent

Segments of Secants, Chord and Tangent

Segments of Secants and Chord: Secants AB and CD intersect inside the circle in fig (a) and outside the circle in fig (b).

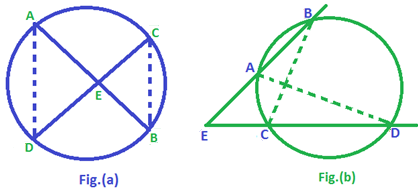
From the figure, we have 

∠DCB = ∠DAB

and ∠ADC = ∠ABC

Hence ΔADE ~ ΔCBE

∴ \(\frac{AE}{CE}=\frac{DE}{BE}\).

AE x BE = CE x DE

Segments of Tangent: In fig (c), AD is secant and AB is tangent. Therefore,

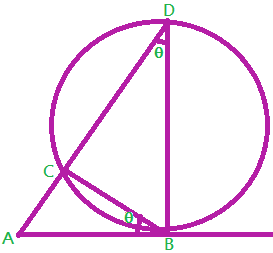
ΔABD ~ ΔACB

∴ \(\frac{AB}{AC}=\frac{AD}{AB}\).

AB² = AC x AD

Example: If a line is drawn through a fixed-point P (α, β) to cut the circle x² + y² = a² at A and B, then find the value of PA.PB.

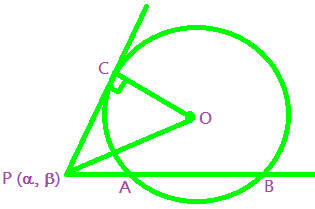
From the figure,

x² + y² = a²

PA. PB = constant

Also PA. PB = PC²

But PC² = OP² – OC²

= α² + β² – a²

PA. PB = α² + β² – a².