The Second law of thermodynamics states that the state of entropy of the universe, as an isolated system, will always increase over time. The second law also states that the changes in the entropy in the universe can never be negative.
Why is it that when you leave an ice cube at room temperature, it begins to melt? Why do we get older and never younger? And, why is it whenever rooms are cleaned, they become messy again in the future? Certain things happen in one direction and not the other, this is called the “arrow of time” and it encompasses every area of science. The thermodynamic arrow of time (entropy) is the measurement of disorder within a system, the change of entropy suggests that time itself is asymmetric with respect to order of an isolated system, a system will become more disordered, as time increases.
Derivation: To understand why entropy increases and decreases, it is important to recognize that two changes in entropy have to consider at all times. The entropy change of the surroundings and the entropy change of the system itself. Given the entropy change of the universe is equivalent to the sums of the changes in entropy of the system and surroundings:-
\( \Delta {{S}_{univ}}\,=\,\Delta {{S}_{sys}}\,+\,\Delta {{S}_{surr}}\)
\( \Delta {{S}_{univ}}\,=\,\frac{{{q}_{sys}}}{T}\,+\,\frac{{{q}_{surr}}}{T}\)
In an isothermal reversible expansion, the heat q absorbed by the system from the surroundings is:-
\( {{q}_{rev}}\,=\,nRT\,\ln \,\frac{{{V}_{2}}}{{{V}_{1}}}\)
Since the heat absorbed by the system is the amount lost by the surroundings, \( {{q}_{sys}}\,=\,-\,{{q}_{surr}}\) . Therefore, for a truly reversible process, the entropy change is:-
\( \Delta {{S}_{univ}}\,=\,\frac{nRT\,\ln \,\frac{{{V}_{2}}}{{{V}_{1}}}}{T}\,+\,\frac{-nRT\,\ln \,\frac{{{V}_{2}}}{{{V}_{1}}}}{T}\,=\,0\)
If the process is irreversible however, the entropy change is:-
\( \Delta {{S}_{univ}}\,=\,\frac{nRT\,\ln \,\frac{{{V}_{2}}}{{{V}_{1}}}}{T}\,>\,0\)
If we put the two equations for together for both types of processes, we are left with the second law of thermodynamics,
\( \Delta {{S}_{univ}}\,=\,\Delta {{S}_{sys}}\,+\,\Delta {{S}_{surr}}\ge 0\)
Where equals zero for a truly reversible process and is greater than zero for an irreversible process. In reality, however, truly reversible processes never happen (or will take an infinitely long time to happen), so it is safe to say all thermodynamic processes we encounter everyday are irreversible in the direction they occur.
The Second law of thermodynamics can also be stated that all spontaneous processes produce an increase in the entropy of the universe.
We now present two statements of the Second Law of Thermodynamics, the first regarding a heat engine, and the second regarding a heat pump. Neither of these statements can proved, however have never been observed to be violated.
The Kelvin – Plank Statement: It is impossible to construct a device which operates on a cycle and produces no other effect than the transfer heat from a single body in order to produce work.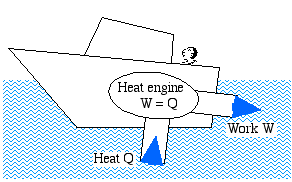
We prefer a less formal description of this statement in terms of a boat extracting heat from the ocean in order to produce its required propulsion work.
The Clausius Statement: It is impossible to construct a device which operates on a cycle and produces no other effect than the transfer of heat from a cooler body to a hotter body.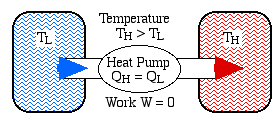
Example: A reversible heat engine receives 3000 KJ of heat from a constant temperature source at 650 K. If the surrounding is at 295K. Find the
- The Availability of heat energy.
- Unavailability heat.
Solution:
\( Change\,in\,entropy\,(\Delta S)\,\,=\,\,\int{\frac{\Delta Q}{T}}\)
\( =\,\,\,\frac{{{Q}_{1}}}{({{T}_{1}}+{{T}_{0}})}\)
\( =\,\,\frac{3000}{(650+295)}\)
\( =\,3.17\,KJ/K\)
The availability of heat energy,
\( A\,=\,{{Q}_{1}}-{{T}_{0}}(\Delta S)\)
\( =3000\,-\,295(3.17)\)
\( =\,2064.85\,KJ\)
\( Unavailable\,Heat\,\,=\,\,{{T}_{0}}\,(\Delta S)\)
\( =\,295(3.17)\)
\( =\,935.15\,KJ.\)