Rolling of a Body on an Inclined Plane
A rigid body of radius of gyration (k) and radius (R) rolls down a plane inclined at an angle (θ) with the horizontal. When a body is placed on an inclined plane, it tries to slip down and hence a static friction (f) acts upwards. This friction provides a torque which causes the body to rotate. Let, a be the linear acceleration of centre of mass and α be the angular acceleration of the body.
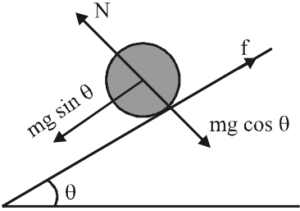
From force diagram: For linear motion parallel to the plane,
mg sinθ – f = ma
For rotation around the axis through centre of mass, net torque = Iα.
fR = (mk²)α
As there is no slipping, the point of contact of the body with the plane is instantaneously at rest.
v = Rω and a = Rα
Solving the following three equation for a and f:
mg sinθ – f = ma … (1)
fR = mk²α … (2)
a = Rα … (3)
\(a=\frac{g\,\sin \theta }{\left( 1+\frac{{{k}^{2}}}{{{R}^{2}}} \right)}\) and \(f=\frac{mg\,\sin \theta }{\left( 1+\frac{{{R}^{2}}}{{{k}^{2}}} \right)}\).
We can also derive the condition for pure rolling, to avoid slipping f ≤ μsN.
\(\frac{g\,\sin \theta }{1+\frac{{{R}^{2}}}{{{k}^{2}}}}\le {{\mu }_{s}}mg\,\sin \theta \).
\({{\mu }_{s}}\ge \frac{\tan \theta }{\left( 1+\frac{{{R}^{2}}}{{{k}^{2}}} \right)}\).
This is the condition of μs. So, that the body rolls without slipping.
