Rolling motion is a combination of rotation and translation.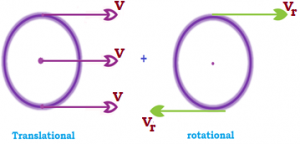
All the particles on a rolling body have two kinds of velocity.
Translational, which is the velocity of centre of mass
Linear velocity on account of rotational motion
When a rigid body moves on a surface
Its motion is said to be pure rolling if there is no slipping between the points of contact of two surfaces.
It motion is said to be rolling with slipping. If there is slipping between the points of contact of two surfaces.
Consider a uniform sphere which is rolling on a rough plank as shown and let P₀ and P₁ be the point of contact of sphere and plank, respectively.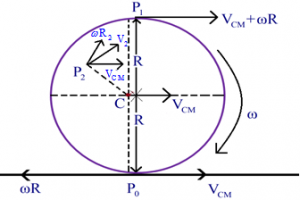
In the figure every point have two velocities, one in the direction of velocity of centre of mass and other perpendicular to the line joining and the point.
At point Pₒ have two opposite velocities, and if condition of no slipping is there then it must have zero velocity, so Vcm = wR.
At P₁ both the velocities in same direction, so add up and at other point, add both the velocities vectorially to get the resultant point Pₒ Instantaneously at rest.
Kinetic energy of Rolling motion:-
KErolling = KEtranslatoin + KErotation
KErolling =1/2 ICM w² +1/2 m VCM ²
Total kinetic energy of a rolling object is the sum of the rotational kinetic energy about the centre of mass and translational kinetic energy of the centre of mass.
Substitute,
I = mk² (where k is radius of gyration)
Vcm = Rw
KErolling =1/2 mk²w² + ½ mR² w²
= 1/2 mk²w² +R²/R² + 1/2 mR² w²
= mR² w² [1+K²/R²]
KErolling =1/2 m VCM ² [1+K²/R²]