Rolling Motion
Rolling Motion is a composite motion, in which the body rotates about a moving axis as it translates from one position to another. In our daily life, we observe various moving cars, bikes, rickshaws etc. All these circular wheels possess rolling motion. A body such as a sphere or a wheel or primarily a circular body which is rolling over a horizontal surface undergoes rolling motion and at every instant, there is a single point of contact.
Let us assume that a disc shaped body is rolling over a surface without slipping. In other words, at any particular instant of time, the part of the disc in contact with the surface is at rest with respect to the surface.
Rolling motion is a combination of translational and rotational motion. For a body, the motion of the centre of mass is the translational motion of the body. During rolling motion of a body, the surfaces in contact get deformed a little temporarily. Due to this deformation a finite are of both bodied comes in contact with each other. The overall effect of this phenomenon is that the component of the contact force parallel to the surface opposes motion resulting in friction.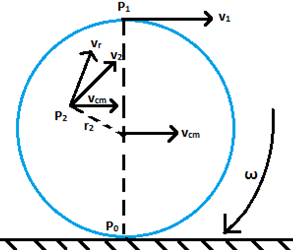
Let, Vcm is the velocity of the centre of mass of a disc shaped body. Since for a rolling disc, the centre of mass would lie at the geometric centre C, the velocity of body or velocity of C is Vcm, which is parallel to the rolling surface. The rotational motion of the body occurs about its axis of symmetry, therefore, the velocity at any point P₀, P₁ and P₂ of the body comprises of two parts, translational velocity Vcm and due to rotational motion, and it has linear velocity Vr.
Where,
Vr = rω,
ω = the angular velocity of the rolling disc.
Vr is perpendicular to radius vector at any point lying on the disc with respect to the geometric centre C. Consider the point P0 on the disc. Vr is directed opposite to Vcm and at this point Vr = rω.
Where,
R = radius of the disc.
Therefore, for the disc, the condition for rolling without slipping is given by Vcm = rω,
The kinetic energy of such a rolling body is given by the sum of kinetic energies of translational motion and rotation.
K.E = ½ mvcm² + ½ Iω²
Where,
m = Mass of the body,
Vcm = Rotational motion,
I = moment of Inertia,
ω = angular velocity of the rolling body.
Rolling motion is a composite motion, in which a body undergoes both translational and rotational motion. The wheel of a car, for example, rotates about a moving axis and at the same time translates a net distance. Rolling motion being superposition of two types of motion, presents a different context of motion, which needs visualization from different perspectives. Importantly, different parts of the wheel are moving with different velocities, depending on their relative positions with respect to the centre of mass or the point of contact with the surface.