RMS Value:
RMS value is defined on the basis of the heating effect of the waveform. The ac voltage at which heat produced in an ac circuit is equal to heat produced in the dc circuit is called as Vrms, provided both ac circuit ac circuit and dc circuit have equal value of resistance and operated for same time period.
Pdc = I²R
Wdc = I²Rt
And Pac = i²R
So, Wac = i²Rt
As per definition Wac = Wdc
The general formula for finding the rms value is,
\({{V}_{rms}}=\sqrt{\frac{1}{T}~\underset{0}{\overset{T}{\mathop \int }}\,{{V}^{2}}dt}\).
Or for sinusoidal waveform
\({{V}_{rms}}=\sqrt{\frac{1}{2\pi }~\underset{0}{\overset{2\pi }{\mathop \int }}\,{{V}^{2}}~d\omega t}\).
Here we shall now derive rms value for some waveforms which are commonly encountered.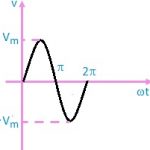 \({{V}_{rms}}=\sqrt{\frac{1}{2\pi }~\underset{0}{\overset{2\pi }{\mathop \int }}\,{{V}^{2}}d\omega t}=\sqrt{\frac{1}{2\pi }~\underset{0}{\overset{2\pi }{\mathop \int }}\,{{\left( {{V}_{m}}~sin\omega t \right)}^{2}}~d\omega t}\).
\({{V}_{rms}}=\sqrt{\frac{1}{2\pi }~\underset{0}{\overset{2\pi }{\mathop \int }}\,{{V}^{2}}d\omega t}=\sqrt{\frac{1}{2\pi }~\underset{0}{\overset{2\pi }{\mathop \int }}\,{{\left( {{V}_{m}}~sin\omega t \right)}^{2}}~d\omega t}\).
\(=\sqrt{\frac{1}{2\pi }~\underset{0}{\overset{2\pi }{\mathop \int }}\,V_{m}^{2}\left( 1-\cos 2\omega t \right)d\omega t}\).
\({{V}_{rms}}=\frac{{{V}_{m}}}{\sqrt{2}}\).
Average Value:
Average value is defined on the basis of the charge transfer in the circuit. The ac voltage, at which the charge transfer in ac circuit is equal to charge transfer dc circuit, is called as Vavg provided both ac and dc circuits are operated for same time period and having equal value of resistance. I = V/R; i = v/R
I = V/R; i = v/R
I = Q/t, Qac = i x t
Qdc = I x t
As per definition,
Qdc = Qac
The average value can be calculated as, Vavg = 1/T T∫₀ V(t) dt
