Rigid body
A rigid body is an extended area of material that includes all the points inside it, and which moves so that the distances and angles between all its points remain constant.
Rigid body is an idealization of a solid body where the deformations occurring on the body are neglected. In other words, the distance between any two given points of a rigid body remains a constant regardless of the external force acting upon it.
Motion of a Rigid body:
Translational Motion: A Rigid body is said to undergo pure translational, if it moves such that all its particles along the parallel paths. In this motion all particles have same distance, displacement, velocity and acceleration. If these parallel paths are straight lines, the motion is said to be a rectilinear translation. If the paths are curved lines, the motion is a curvilinear translation.
Rotational Motion: A rigid body is said to undergo pure rotational, if it moves such that its constituent particles move along circular arcs, the centres of which lie on a straight line perpendicular to the plane of the arcs. This straight line is known as the axis of rotation and the rigid body is said to undergo pure rotation about this axis. In this case all the particles have the same angular displacement, angular velocity and angular acceleration.
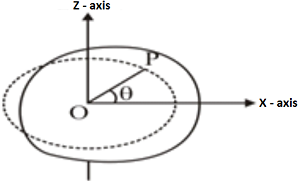
Rotational Kinematics of Rigid body: Consider a rigid body rotating about a given fixed line. Take this line as z – axis. The angular position of the body at any time t is said to be θ. The rotation of the rigid body is measured by the rotation of the line OP from its initial position.
Now suppose the angular position of the body at any time t is θ. During a time Δt, it further rotates through Δθ, so that its angular position becomes θ + Δθ. The average angular velocity during the time interval Δt is
\(\omega \,=\,\frac{\Delta \theta }{\Delta t}\)
The instantaneous angular velocity at time t is \(\omega \,=\,\frac{d\theta }{dt}\).
Angular Acceleration:
\(Average\,\,Angular\,\,Acceleration\,\,(\overrightarrow{{{\alpha }_{av}}})\,\,=\,\,\frac{\overrightarrow{\omega }({{t}_{2}})\,-\,\overrightarrow{\omega }({{t}_{1}})}{{{t}_{2}}\,-\,{{t}_{1}}}\)
Where,
\(\overrightarrow{\omega }(t)\) = Instantaneous Angular Velocity at time t.
The instantaneous angular acceleration is defined using calculus, by the expression:
\(\overrightarrow{\alpha }\,=\,\frac{d\overrightarrow{\omega }}{dt}\).
All the quantities referred to above are defined with respect to an axis fixed in direction.
