Sometimes we are interested to replace a relatively complicated resistor combinations with a single equivalent resistor, especially when we are not interested in the current, Voltage or power associated with any of the individual resistors in the combinations. All the current, voltage and power relationships in the remainder of the circuit will be unchanged.
Consider the series combinations of N – resistors.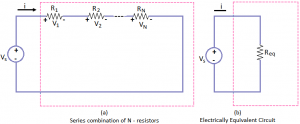
First apply KVL,vs = v₁ + v₂ + … + vN
And then ohm’s law,
vs = R₁i+ R₂i + … + RNi
= (R₁ + R₂ + … + RN) i
Now compare this result with the simple equation applying to the equivalent circuit.
vs = Reqi
Thus, the value of the equivalent resistance for N – series resistors is
Req = R₁ + R₂ + … + RN
Similar simplification can be applied to parallel circuits. A circuit containing N – resistors in parallel, as in leads to KCL equation,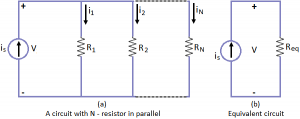
is = i₁ + i₂ + … + iN
Or \({{i}_{s}}=\frac{v}{{{R}_{1}}}+\frac{v}{{{R}_{2}}}+\ldots+\frac{v}{{{R}_{N}}}=\frac{v}{{{R}_{N}}}\)
Thus, \(\frac{1}{{{R}_{eq}}}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}+\ldots +\frac{1}{{{R}_{N}}}\)