Resistors in Series and Parallel
In an electric circuit, the different components can be connected either in series or in parallel to produce different resistive networks. Sometimes, in the same circuit, resistors can be connected in parallel and series, across different loops to produce a more complex resistive network.
In the end, however, the total resistance should be known. It is important to know how to do this because resistors never exist in isolation. They are always part of a larger circuit that will have many resistors connected in different combinations.
So how do we calculate this total resistance for resistors in series and parallel circuits?
Resistors in Series: They are said to be connected in series when the same amount of current flows through them. The corollary is also true, i.e., if they are connected in series then the same amount of current flows through them.
![]()
If the resistors in a circuit are all connected in series, like the figure given above, then the total resistance of the system is given by the following relation.
RTotal = R₁ + R₂ + … + Rn
The total resistance of the system is just the sum total of individual resistances.
For Example: A resistor having an electrical resistance value of 100 W, is connected to another resistor with a resistance value of 200 W. The two resistances are connected in series. What is the total resistance across the system?
Here,
R₁ = 100 W
R₂ = 200 W
RTotal = 100 + 200 = 300 W
Resistors in Parallel: They are said to be connected in parallel when the same voltage flows through them. The corollary of this is true as well.
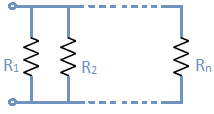
The figure above shows ‘n’ number of resistors connected in parallel. The total resistance here is given by the following relation.
\(\frac{1}{{{R}_{Total}}}\,=\,\frac{1}{{{R}_{1}}}\,+\,\frac{1}{{{R}_{2}}}\,+\,……\,+\,\frac{1}{{{R}_{n}}}\).
Here, the reciprocal of the total resistance of the system is the sum of the reciprocals of resistances of the individual resistor in the circuit.
For the problem given above, what if the resistors were connected in parallel instead of in series? What is the total resistance in that case?
\(\frac{1}{{{R}_{Total}}}\,=\,\frac{1}{100}\,+\,\frac{1}{200}\,\),
\(\frac{1}{{{R}_{Total}}}\,=\,\frac{300}{20000}\),
∴ \({{R}_{Total}}\,=\,\frac{20000}{300}\,=\,66.67\Omega \).
