First let us consider a uniform field, for which the lines of force are parallel and equidistance from each other. Let A and B be two points in a uniform electric field of intensity E.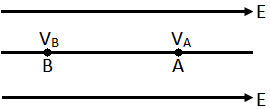
Let WAB, be the work done to carry a test charge q0 from A to B. Let the potential at A and B be VA and VB, respectively. We have already seen that WAB/q₀ = VB – VA
The work done to carry the test charge from A to B is WAB = q₀EAB
q₀EAB/q₀ = VB – VA
E = (VB – VA)/AB
Let the potential difference VB – VA = V and AB = l
Then E = V/l
The electric field between the two plates separated by a distance d is uniform. If the potential difference between the plates is V. then E = v/ d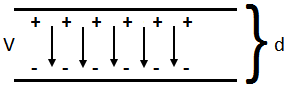
To show that E = – dV/dx
Let us consider a non-uniform electric field. The electric intensity varies from one point to another. Let A and B be two points which are very close to each other so that the electric intensity is almost constant.
Let OB = x, AB = dx and OA = x + dx. The potential at B is V and that at A is V – dV. Consider test charge q0 kept at A where electric intensity is E. The force acting on q0 charge at A is F = q0E. The work done to carry q0 charge from A to B through an infinitesimally small displacement dx is dW = F (-dr)
dW = – q₀ Edx, dW/q₀ = -Edx … (1)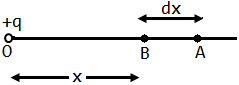
But dW/q₀ is the work done in carrying unit test charge from A to B which is the potential difference between the points A and B.
dW/q₀ = VB – VA = V – (V – dV) = dV
From equation (1) dW/q₀ = – Edx
Hence dV = – Edx
E = – dV/dx
dV/ dx is the rate of change of electrostatic potential with distance and is called the potential dx gradient. Thus the electric intensity at a point in an electric field is the negative potential gradient.