Relation between Angular Velocity and Linear Velocity
What is Angular Velocity?
Angular velocity is the rate of velocity at which an object or a particle is rotating around a center or a specific point in a given time period. It is also known as rotational velocity. We can also define the angular velocity of a particle as the rate at which the particle rotates around a center point i.e., the time rate of change of its angular displacement relative to the origin.
What is Linear Velocity?
Linear velocity is the rate of change of the position of an object that is traveling along a straight path. Because any moving object has a linear velocity, this measurement shows up very often in everyday life. For instance, if a person goes for a walk, drive, run, or bike ride, there is linear velocity.
Relation between Angular Velocity and Linear Velocity:
Let us consider a body P moving along the circumference of a circle of radius r with linear velocity V and angular velocity ω as shown in fig. Let it move from P to Q in time dt and dθ be the angle swept by the radius vector.
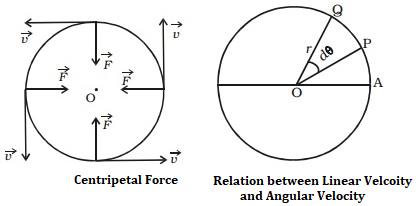
Let, PQ = ds be the arc length covered by the particle moving along the circle, then then angular displacement (d), θ is expressed as dθ = ds/r, But ds = v dt.
\(\frac{d\theta }{dt}=\frac{v}{r}\) i.e. Angular velocity (ω) = v/ r
v = ωr
In vector notation: \(\overrightarrow{v}=\overrightarrow{\omega }\times \overrightarrow{r}\).
Thus, for a given angular velocity, the linear velocity of the particle is directly proportional to the distance of the particle from the center of the circular path.
