Radical Axis and it’s Properties
Radical Axis: The radical axis of two circles is the locus of the point which moves such that the lengths of the tangents drawn from it to the two circles are equal.
Consider,
S ≡ x² + y² + 2gx+ 2fy +c = 0 … (1)
and S ≡ x² + y² + 2g₁x+ 2f₁y + c₁ = 0 … (2)
Let P (x₁, y₁) be a point such that |PA| = |PB|
i.e., \(\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}+2g{{x}_{1}}+2f{{y}_{1}}+c}=\sqrt{{{x}_{1}}^{2}+2{{g}_{1}}{{x}_{1}}+2{{f}_{1}}{{y}_{1}}+{{y}_{1}}^{2}}\).
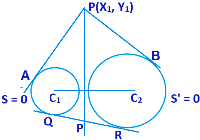
On squaring in both sides
x₁² + y₁² + 2gx₁ + 2fy₁ + c = x₁² + y₁² + 2g₁x₁ + 2f₁y₁ + c₁
2 (g – g₁) x₁ + 2 (f – f₁) y₁ + c – c₁ = 0
Which is the required equation of the radical axis of the given circles. Clearly, this is a straight line.
Properties of the Radical Axis:
1. The Radical Axis is Perpendicular to the Line joining the Centers of the given Circles:
Slope of \({{C}_{1}}{{C}_{2}}=\frac{-{{f}_{1}}+f}{-{{g}_{1}}+g}=\frac{f-{{f}_{1}}}{g-{{g}_{1}}}\) = m₁ (say).
Slope of radical axis = \(-\frac{(g-{{g}_{1}})}{f-{{f}_{1}}}\) = m₂ (say).
∴ m₁m₂ = -1.
Hence, C₁C₂ and radical axis are perpendicular to each other.
2. Radical Axis Bisects the Common Tangent of Two Circles: Let QR be the common tangent. If it meets the radical axis P, then PQ and PR, are two tangents to the circles.
Hence, PQ = PR, since the lengths of tangents are equal from any point on the radical axis. Hence, the radical axis bisects the common tangent QR.
