Properties of Tangents – Parabola
(i) Point of Intersection of Tangent at any Two Points on the Parabola.
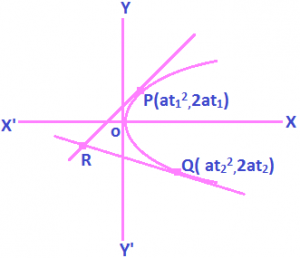
Let the equation of the parabola be y² = 4ax.
The two points on the parabola are P ≡ (at₁², 2at₁) and Q ≡ (at₂², 2at₂).
The equation of the tangents at P and Q are, respectively,
t₁y = x + at₁²
t₂y = x + at₂²
solving these equations, we get
x = at₁t₂
y = a(t₁ + t₂)
thus, the coordinates of the point of intersection of tangents at (at₁², 2at₁) and (at₂², 2at₂) are
(at₁ t₂, a(t₁ + t₂) ).
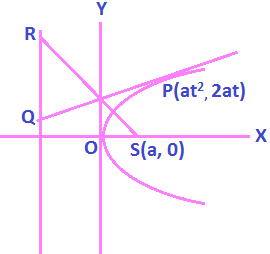
(ii) Locus of Foot of Perpendicular from Focus upon any Tangent is Tangent at Vertex:
The equation of the tangent to the parabola y² = 4ax at point P(t) is ty = x+ at².
It meets the y- axis at Q(0, at) Now mSQ = (at – 0)/ (0 – a) = -t
The slope of tangent PQ is 1/t