Principle of Superposition of Waves

The Principle of Superposition states that when two waves of the same kind meet at a point in space, the resultant displacement at that point is the vector sum of the displacements that the two waves would separately produce at that point. Interference refers to the superposing of two or more coherent waves to produce regions of maxima and minima in space, according to the principle of superposition. Constructive interference occurs when two or more waves arrive at the screen in phase with each other, such that the amplitude of the resultant wave is the sum of the amplitude of the individual waves. Destructive interference occurs when the two or more waves arrive π out of phase with each other.

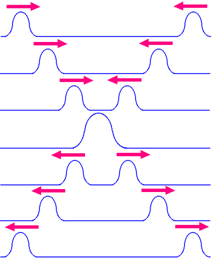
The principle of superposition, the net response for all linear systems at a given time for a given place, caused by two or more stimuli, is the sum of responses which would have been caused by each stimulus individually. So, if the response produced by input A is X and that produced by input B is Y, then the response produced by input A + B is X + Y.

Considering two waves, travelling simultaneously along the same stretched string in opposite directions as shown in the figure above. We can see images of waveforms in the string at each instant of time. It is observed that the net displacement of any element of the string at a given time is the algebraic sum of the displacements due to each wave.

Let us say two waves are travelling alone and the displacements of any element of these two waves can be represented by y₁(x, t) and y₂(x, t). When these two waves overlap, the resultant displacement can be given as y(x, t).

Mathematically, y (x, t) = y₁(x, t) + y₂(x, t).

As per the principle of superposition, we can add the overlapped waves algebraically to produce a resultant wave. Let us say the wave functions of the moving waves are

y₁ = f₁ (x – vt),

y₂ = f₂ (x – vt),

. . . . . . . . . .

y_n = f_n (x – vt)

Then the wave function describing the disturbance in the medium can be described as

y = f₁ (x – vt) + f₂ (x – vt) + … + f_n (x – vt)

Or y = ⁿΣ ᵢ₌₁ fᵢ (x – vt)

Let us consider a wave travelling along a stretched string given by y₁ (x, t) = A sin (kx – ωt) and another wave, shifted from the first by a phase φ, given as y₂ (x, t) = A sin (kx – ωt + φ).

From the equations we can see that both the waves have the same angular frequency, same angular wave number k, hence the same wavelength and the same amplitude A.

Now, applying the superposition principle, the resultant wave is the algebraic sum of the two constituent waves and has displacement y (x, t) = A sin (kx – ωt) + A sin (kx – ωt + φ).

As sin A = sin B = 2 sin ½ (A + B) cos ½ (A – B).

The above equation can be written as, y (x, t) = [2A cos ½ φ] sin (kx – ωt + ½ φ).

The resultant wave is a sinusoidal wave, traveling in the positive X direction, where the phase angle is half of the phase difference of the individual waves and the amplitude as [2 cos ½ φ] times the amplitudes of the original waves.