This is applicable only to a plane lamina. The moment of inertia of a plane lamina about an axis perpendicular to its plane is equal to the sum of the moments of inertia of the lamina about any two mutually perpendicular axes, passing in its own plane, intersecting each other at the point through which the perpendicular axis passes.
It states that for any plane body, for example a rectangular sheet the moment of inertia about any of its axis which are perpendicular to the plane is equal to the sum of the moment of inertia about any two perpendicular axis in the plane of the body which intersect the first axis in the plane, this theorem is used when the body is symmetric in shape about two out of three axis, if moment of inertia about two of the axis are known the moment of inertia about the third axis can be found using the expression.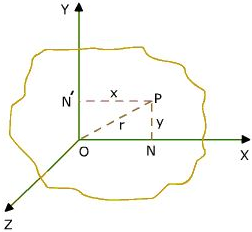
Let us consider a plane lamina lying in the XOY plane. The lamina is made up of a large number of particles. Consider a particle of mass ‘m’ at P. From P, PN and PN¹ are drawn perpendicular to X-axis and Y-axis, respectively.
Now, PN’ = x, PN = y
Moment of inertia about X-axis = my²
Moment of inertia of the whole of lamina about X-axis is Ix = ∑ my²
Moment of inertia of the whole of lamina about Y-axis is Iy = ∑ mx²
Moment of inertia of the whole of lamina about Z-axis is Iz = ∑ mr²
But, r² = x² + y²
∴ Iz = ∑ m (x² + y²)
Iz = ∑ mx² + ∑ my²
(OR)
Iz = Ix + Iy.
The perpendicular axis theorem helps in applications where we don’t have access to one axis of a body and it is vital for us to calculate the moment of inertia of the body in that axis.
How to find the Perpendicular Axis Theorem?
Example: Let I be the moment of Inertia of a uniform square plate about an axis AB that passes through its centre and is parallel to two of its side, CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle θ with AB. The moment of Inertia of the plate about the axis CD is then equal to?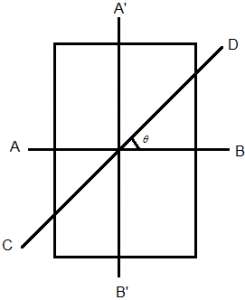
Solution: From symmetry IAB = IA’B’ and ICD = IC’D’, from theorem of Perpendicular axis,
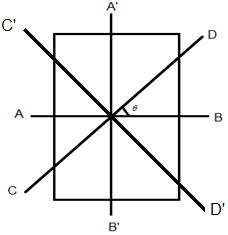Izz = IAB + IA’B’
= ICD + IC’D’
= 2 IAB
= 2 ICD