This law states that pressure in a fluid in equilibrium is the same everywhere, if the effect of gravity can be neglected.
Proof:
We can show that pressures at any two points C and D in a liquid in equilibrium state of rest in a vessel are the same.
Let us imagine a right circular cylinder in the liquid with the line CD as axis and points C and D as centres of the flat end faces of the cylinder.
Let us consider the liquid inside the cylinder which is an equilibrium under the action of forces exerted by the liquid outside the cylinder.
These forces are perpendicular to the surfaces of the cylinder everywhere, as shown.
It is clear that the forces F1 and F2 on the flat faces at C and D are perpendicular to the forces on the curved surface of the cylinder.
Since the liquid is in equilibrium, the sum of all forces acting on the cylinder must be zero. As such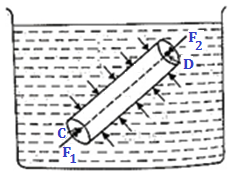
F1 = F2
If p1 and p2 be the pressures on the flat faces at C and D, and A be the area of cross section of each face, then
F1 = p1A and F2 = p2A
.·. p1 = p2
Thus, Pascal’s law is proved. A similar argument can be made to show that the pressure at any point does not depend on the direction of the surface on which it acts.
A natural consequence of Pascal’s law is that in an enclosed liquid, if pressure is increased in any part of the liquid, then it is transmitted equally to all parts of the liquid.
Application: (Hydraulic Lift)
It is used to lift heavy loads, such as cars at a service station. It is based on the simple principle that when a small force is applied over a piston of small cross-sectional area, then due to transmission of pressure, a large force appears over a piston of large cross-sectional area. This force is used to support and lift heavy weights.
Basically, a hydraulic lift consists of two cylinders of cross-sectional areas A1 and A2 (A1 < < A2) connected by a horizontal pipe. Each cylinder is fitted with air-tight frictionless piston. The cylinders are filled with an incompressible liquid.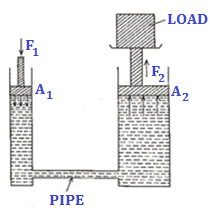
Suppose a force F1 is applied on the piston of smaller area of cross-section A1. Then, the pressure exerted over the liquid is
p = F1/A1
This pressure is transmitted unchanged to the piston of larger cross-sectional area A2. Therefore, the upward force F2 exerted on the larger piston is given by
F2 = p * A2 = F1/A1 * A2
Since A2 > > A1, therefore F2 > > F1. Thus, a heavy load placed on the larger piston is lifted up).