The theorem determines the moment of inertia of a rigid body about any given axis, given that moment of inertia about the parallel axis through the centre of mass of an object and the perpendicular distance between the axes.
The moment of inertia of a body about an axis is equal to its moment of inertia about a parallel axis through its centre of gravity plus the product of the mass of the body and the square of the perpendicular distance between the two parallel axes.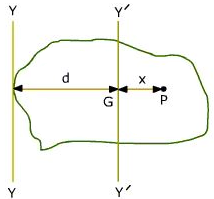
Let ‘I’ be the moment of inertia of a plane lamina about an axis YY. Let ‘G’ be the centre of gravity of the lamina. Y¹Y¹ is an axis parallel to YY and passing through ‘G’. Let ‘Ig’ be the moment of inertia of the lamina about Y¹Y¹.
Let GP = x.
Moment of inertia of the particle about
YY = m (x + d)2
Moment of inertia of the whole of lamina about
YY = I = ∑ m (x + d)²
= ∑ m (x² + d² + 2xd)
⇒ I = ∑ mx² + ∑ md² + ∑ 2mxd
But ∑mx² = Ig, ∑md² = (∑ m)d² = Md²
Also ∑ 2mxd = 2d∑mx
∴ I = Ig + md² + 2d ∑ mx
The lamina will balance itself about its centre of gravity. So the algebraic sum of the moments of the weights of constituent particles about the centre of gravity G should be zero.
∴ ∑ mg x X = 0 or g ∑ mx = 0
⇒ ∑ mx = 0
∴ I = Ig + Md².
The parallel axis theorem can be used to determine the object’s moment of inertia of a rigid body around any axis. This theorem is also known as Huygens – Steiner theorem. According to the parallel axis theorem, there is an affiliation between the inertia of an object rotation around its centre of gravity and an axis parallel to this centre. This theorem can be used to any solid object in rotation, as well as with irregular shapes. For easy understanding, the parallel axis theorem is a relation between the moment of inertia about an axis passing through the centroid, the centre of gravity of a geometrical object of uniform density and the moment of inertia about any parallel axis.