Let us consider a parallel-faced slab whose cross-sectional area is A and length L. Let its faces be maintained at steady temperatures θ1 and θ2. Heat will flow through the slab from the face at higher temperature θ1 to that at the lower temperature θ2. Let us assume that no heat escapes out from the sides of the slab by convection or radiation. Thus, the lines of flow will be at all points normal to the faces of the slab. In these circumstances, under steady state, the quantity of heat Q entering one face in a given time is same as the heat leaving the other face in the same time. Experiment shows that the heat Q is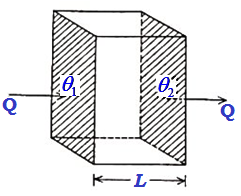 a) Directly proportional to the cross-sectional area A of each face, that is Q α A,
a) Directly proportional to the cross-sectional area A of each face, that is Q α A,
b) Directly proportional to the temperature-difference (θ1 – θ2) between the two faces, that is, Q α (θ1 – θ2),
c) Directly proportional to the time t for which the heat flows, that is, Q α t
d) Inversely proportional to the length 1 of the slab (distance between hot and cold faces), that is, Q α 1/t
Combining the above factors, we get
Q α A (θ1 – θ2) t / l
Q = KA (θ1 – θ2) t / l
Where K is a constant depending on the material of the slab. It is called the “coefficient of thermal conductivity” of the material of the slab. The coefficient of thermal conductivity K of a material is defined as the amount of heat that flows in unit time through unit area of the material perpendicular to the flow under unit temperature-gradient, when the steady state has been reached.
