Non-Removable Discontinuity
If \(\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f(x)\ne \underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f(x)\), then f(x) is said to have the first kind of non-removable discontinuity.
Consider the function f(x) = 1/x. the function is not defined at x = 0. It cannot be extended to a continuous function whose domain is R. since no matter what value is assigned at 0, the resulting function will not be continuous. A point in the domain that cannot be filled in so that the resulting function is continuous is called a Non-Removable Discontinuity.
Graphical view of Non-Removable Discontinuity:
Both the limits are finite and equal: Consider the function f(x) = [x] – greatest integer function. As shown in the graph has jump of discontinuity at all integral value of x.
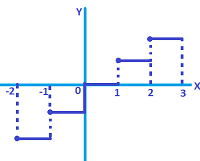
At least one of left and right limit is infinity or vertical asymptote
Consider the function f(x) = tanx
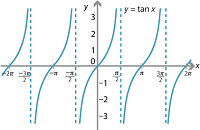
Here, the function is not defined at point \(\pm 3\frac{\pi }{2}\) and near these points, the function becomes both arbitrarily large and small. since the function is not defined at these points, it cannot be continuous.
Example: Find the points of discontinuity of the \(f(x)=\frac{1}{2\sin x-1}\).
Solution: Given that \(f(x)=\frac{1}{2\sin x-1}\).
f(x) is discontinuous when
2sinx – 1 = 0
Sinx = ½
x = sin⁻¹ (½)
x = π/6 (or) 5π/6
The general solution is \(2n\pi \pm \frac{\pi }{6}\) (or) \(2n\pi \pm \frac{5\pi }{6}\), n ϵ z.
