The maximum permissible speed of a car on a banked rough road can be obtained as under.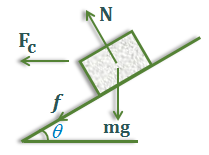
Ncosθ = mg + fsinθ
Nsinθ + fcosθ = mv²/R
If v = vmax then, f = fmax = μsN
On substituting then simplifying we get
\({{v}_{max}}={{\left( \left( \frac{\left( {{\mu }_{s}}+tan\theta \right)}{\left( 1-{{\mu }_{s}}tan\theta \right)} \right)Rg \right)}^{1/2}}\).
EXAMPLE 1:- A small block of mass m is moving over a smooth horizontal surface on a circular path at some moment. Length of string is L and velocity of block at some moment behind the tension in the string.
Solution: Here Tension provides, the required centripetal force
T = mv²/r = mvₒ²/L
EXAMPLE 2:- Find the tangential acceleration of the bob of mass m at a moment when string makes angle θ with vertical as shown.
Solution: Let us make F.B.D. of bob, tension is radial, only force along tangent is
FT = mgsinθ
aT = F/m = gsinθ