Motion of a car on banked road
Friction is not always reliable at circular turns if high speeds and sharp turns are involved. To avoid dependence on friction, the roads are banked at the turn so that the outer part of the road is somewhat lifted up as compared to the inner part.
The surface of road and hence, even the normal force of contact make an angle θ with horizontal and vertical respectively.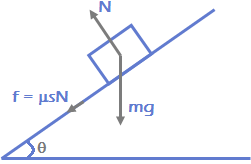
∴ N sinθ = \(\frac{m{{v}^{2}}}{r}\),
N cosθ = mg
∴ \(\tan \,\,\theta \,\,=\,\,\frac{{{v}^{2}}}{rg}\).
The angle θ depends on the speed of the vehicle as well as the radius of the turn. Roads are banked for the average expected speed of the vehicles. If the speed varies slightly from the average expected speed, then the self-adjustable friction comes into play.
If there is a great variation from the average expected speed, even maximum friction cannot prevent the vehicle from slipping.
When θ is small,
\(\tan \,\,\theta \,\,\approx \,\,\sin \theta \,\,=\,\,\frac{{{v}^{2}}}{rg}\,\,=\,\,\frac{height}{width\,\,of\,\,road}\),
We will now repeat the analysis when friction does comes into play, which is usually the case.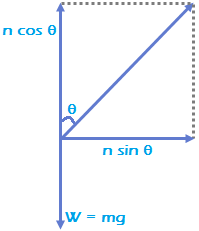
mg + F sinθ = N cosθ
F = μ N
mg = N cosθ – μ N cosθ … (1)
\(\frac{m{{v}^{2}}}{r}\) = N sinθ + μ N cosθ … (2)
Divide equation (2) by equation (1)
\(\frac{{{v}^{2}}}{rg}\,\,=\,\,\frac{\sin \,\theta \,+\,\mu \,\cos \,\theta }{\cos \,\theta \,-\,\mu \,\sin \,\theta }\),
∴ \(v\,\,=\,\,\sqrt{\frac{\tan \,\theta \,+\,\mu }{1\,\,-\,\,\mu \,\tan \,\theta }rg}\).
How to find the motion of a car on banked road?
Problem: Two banked curves have the same radius. Curve A is banked at 130, curve B at 190. A car can travel around curve A without relying on friction at a speed of 18m/sec. at what speed can this car travel around curve B without relying on friction?
Solution: We know that,
\({{v}_{A}}\,\,=\,\,\sqrt{rg\,\tan (\theta )}\,\,=\,18\,m/\sec \),
\({{v}_{A}}\,\,=\,\,\sqrt{rg\,\tan \,({{13}^{0}})}\,\,=\,\,18\,m/\sec \),
\({{v}_{B}}\,=\,\sqrt{rg\,\tan \,({{19}^{0}})}\,=\,?\),
So,
\({{v}_{B}}\,=\,\,18\,m/\sec \,\,\,\times \,\,\,\frac{\sqrt{rg\,\tan \,({{19}^{0}})}}{\sqrt{rg\,\tan \,({{13}^{0}})}}\),
\({{v}_{B}}\,\,=\,\,18\,m/\sec \,\,\,\times \,\,\frac{\sqrt{\tan \,({{19}^{0}})}}{\sqrt{\tan \,({{13}^{0}})}}\),
vB = 22 m/sec.