Lens Maker’s Formula

Lens is a transparent medium bounded by two surfaces, at least one of them must be curved. A relation between the focal length of a lens, radii of curvature of two surfaces and the refractive index of the material is called lens maker’s formula.

Lens Maker’s Formula: Consider the thin lens shown here with the two refracting surfaces having radii of curvature equal to R₁ and R₂ respectively. The refractive indices of this surrounding medium and of the material of the lens are n₁ and n₂ respectively. Now using the result that we obtained for refraction at single spherical surface we get,

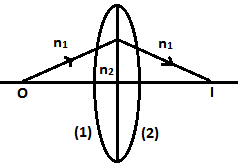
For First Case: \(\frac{{{n}_{2}}}{{{v}_{1}}}\,-\,\frac{{{n}_{1}}}{u}\,=\,\frac{{{n}_{2}}-{{n}_{1}}}{{{R}_{1}}}\) … (1)

For Second case: \(\frac{{{n}_{1}}}{v}\,-\,\frac{{{n}_{2}}}{{{v}_{1}}}\,=\,\frac{{{n}_{1}}\,-\,{{n}_{2}}}{{{R}_{2}}}\) … (2)

Adding equations (1) and (2), we get:

\(\frac{{{n}_{1}}}{v}\,\,-\,\,\frac{{{n}_{1}}}{u}\,\,=\,\,({{n}_{2}}\,\,-\,\,{{n}_{1}})\left[ \frac{1}{{{R}_{1}}}\,\,-\,\,\frac{1}{{{R}_{2}}} \right]\).

\(\frac{1}{v}\,\,-\,\,\frac{1}{u}\,\,=\,\,\left( {{n}_{2}}\,\,-\,\,{{n}_{1}} \right)\left[ \frac{1}{{{R}_{1}}}\,\,-\,\,\frac{1}{{{R}_{2}}} \right]\).

When, u = ∞, v = f

\(\frac{1}{f}\,\,=\,\,\left[ \frac{{{n}_{2}}}{{{n}_{1}}}\,\,-\,\,1 \right]\left[ \frac{1}{{{R}_{1}}}\,\,-\,\,\frac{1}{{{R}_{2}}} \right]\).

\(\frac{1}{v}\,\,-\,\,\frac{1}{u}\,\,=\,\,\frac{1}{f}\).

A lens is converting if its focal length is positive and diverging if focal length is negative, from this we can conclude that a convex lens need not necessarily be a converging and a concave lens diverging.

Lens maker’s formula limitations:

The lens needs to be thin. This is because the separation between the two refracting surface will also be small.
The medium on either side of the lens needs to be the same.