Length of the Chord – Circle

Length of the Chord – Circle

The length of the chord of the circle S = 0 having P (x₁, y₁) as its midpoint is 2 √|S₁₁|.

Proof: Let AB be the chord of the circle S = 0 having P as its midpoint.

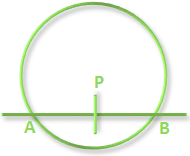
Now PA = PB and PA. PB = |S₁₁|

⇒ PA² = |S₁₁|

⇒ PA = √|S₁₁|

Therefore, length of chord AB = 2 PA

= 2 √|S₁₁|

Example: Find the length of the chord of the circle x² + y² + 2x + 3y + 3 = 0 having (1, 2) as its mid-point.

Solution: Given that

x² + y² + 2x + 3y + 3 = 0

mid-point is P (1, 2)

we know that length of a chord is 2 √|S₁₁|

S₁₁ = x₁² + y₁² + 2x₁ + 3y₁ + 3 = 0

⇒ (1) + 4 + 2 + 6 + 3 = 0

⇒ S₁₁ = 16

Length of a chord is 2 √|S₁₁| = 2 √|16|

= 2 (4)

= 8.