Kepler’s Second Law of Planetary Motion

Kepler’s Second Law of Planetary Motion

Kepler’s second law states that the orbiting satellite will speed up when it gets closer to the object at the focus. This is caused by the increased effect of gravity on the orbiting object as it gets nearer to what pulling it into the orbital path.

The mathematical statement of the law is that the area swept by the planet or rotating object in in giving time is the same, independent of the distance to the object at the focus.

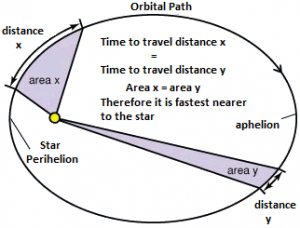
Areas swept in a given time are equal.

Kepler’s second law of planetary motion describes the speed of a planet traveling in an elliptical orbit around the sun. It states that a line between the sun and the planet sweeps equal areas in equal times. Thus, the speed of the planet increases as it nears the sun and decreases as it recedes from the sun.

An imaginary line drawn from the centre of the sun to the centre of the planet will sweep out equal areas in equal intervals of time.

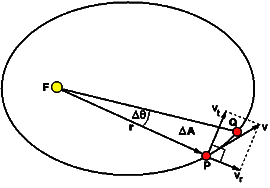
Hence,

ΔA = ½r (r Δ θ) = ½ r²Δθ

Now, we can write:

\(\frac{\Delta A}{\Delta t}\,=\,\frac{1}{2}{{r}^{2}}\frac{\Delta \theta }{\Delta t}\) \(\underset{\Delta t\to 0}{\mathop{\lim }}\,\,\frac{\Delta A}{\Delta t}\,=\,\frac{1}{2}{{r}^{2}}.\underset{\Delta t\to 0}{\mathop{\lim }}\,\,\frac{\Delta \theta }{\Delta t}\)

Taking limits on both sides as Δt → 0

⇒ dA/A = ½ r²ω

⇒ dA/A = l/2m

Now, conservation of angular momentum l is constant.

Thus, dA/A = constant