Angle between Line and a Plane: The angle between a line and a plane is the complement of the angle between the line and normal to the plane.
Thus, if θ is the angle between a lines \(\frac{x-\alpha }{l}=\frac{y-\beta }{m}=\frac{z-\gamma }{n}\).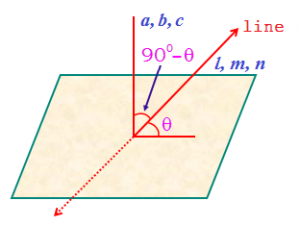
And the plane ax + by + cz + d = 0. Then, the angle between the normal to the plane and the line is (90°- θ).
\(\cos \,\left( {{90}^{0}}-\theta \right)=\frac{al\,+\,bm\,+\,cn}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}\sqrt{{{l}^{2}}+{{m}^{2}}+{{n}^{2}}}}\).
∴ \(\sin \theta =\,\frac{al\,+\,bm\,+\,cn}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}\sqrt{{{l}^{2}}+{{m}^{2}}+{{n}^{2}}}}\).
If the line is parallel to the plane,
∴ al + bm + cn = 0.
If the line is perpendicular to the plane,
∴ \(\frac{l}{a}=\frac{m}{b}=\frac{n}{c}\)
Example: Find the angle between the line \(\frac{x-1}{1}=\frac{y+2}{1}=\frac{z-4}{0}\) and the plane y + z + 2 = 0.
Solution: Let θ be the angle between the line \(\frac{x-1}{1}=\frac{y+2}{1}=\frac{z-4}{0}\) and the plane y + z + 2 = O.
∴ \(\sin \theta =\,\frac{al\,+\,bm\,+\,cn}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}\sqrt{{{l}^{2}}+{{m}^{2}}+{{n}^{2}}}}\).
⇒ \(\sin \theta =\,\frac{1\times 1\,+1\times 0\,+0}{\sqrt{{{1}^{2}}+{{1}^{2}}+0}\sqrt{{{1}^{2}}+{{1}^{2}}+0}}\).
Then,
⇒ Sin θ = ½
⇒ θ = π/6