Intersection of a Line and an Ellipse

Intersection of a Line and an Ellipse

Line: y = mx + c … (1)

Ellipse: \(\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\) … (2)

Solving equations (1) and (2), we get

b²x² + a²(mx + c ) ² = a²b²

i.e., (a²m² + b²) x² + 2a² cmx + a²(c² – b²) = 0.

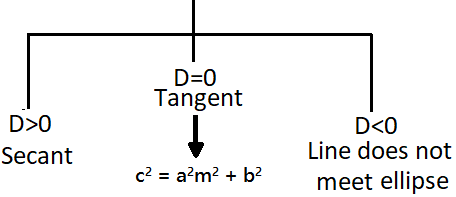
Hence, \(y=mx\pm \sqrt{{{a}^{2}}{{m}^{2}}+{{b}^{2}}}\) are the tangents to the ellipse for all m ϵ R.

Note that there are two parallel tangents for a given m.

If it passes through (h, k), then

\(k=mh\pm \sqrt{{{a}^{2}}{{m}^{2}}+{{b}^{2}}}\).

(k – mh)² = a²m² + b²

 (h² – a²)m² – 2khm + k² – b² = 0 …. (3)

Hence, passing through a given point, there can be a maximum of two tangents.

Equation (3) can be used determine the locus of the point of intersection of two tangents enclosing an angle β. If β = 90, then

m₁ m₂ = -1

k² – b² = a² – h²

x² + y² = a² + b².

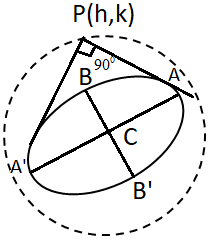
Which is known as the director circle of the ellipse.

Hence, the director circle of an ellipse is the circle whose centre is the centre of the ellipse and whose radius is the length of the line joining the ends of the major and minor axes.