1. Zero order reactions:
⇒ Order of the reaction is zero.
⇒ The reaction in which the rate of reaction is independent of concentration of the reactants.
⇒ Rate of reaction remains constant during the course of reaction.
⇒ No concentration term in the rate law.
A → Products
Initially t = 0 a 0
t = t₁ a – x x
\(\frac{-d{{C}_{R}}}{dt}=\frac{-d\left[ A \right]}{dt}=\frac{-d\left[ a-x \right]}{dt}=k{{\left( a-x \right)}^{0}}=\frac{dx}{dt}\)
dx/ dt = k
dx = k dt
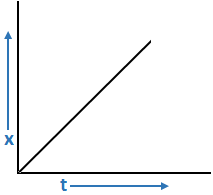
x = kt + c
When t = 0 x = 0 ⇒ C= 0
∴ x = kt
t = t½
x = a/2
a/2 = kt½
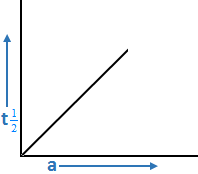
t½ = (a/2) k
a. Graph for x = kt
b. Graph for t½ = a/2K
c. [A₀] – [A] = kt
[A₀] = initial concentration, t = 0
[A]t = concentration, t = t
[A₀] – [A]t = Kt
+ [A]t = -Kt + [A₀]
Half-life of reaction: The time required for the completion of 50% of the reaction is called half-life of the reaction.
Units of rate constant: n A → Products
Rate law is R = K [Conc]n
K = Rate/ (Concentration)n
= mole¹¯ⁿ literⁿ¯¹ sec¯¹
Where n is order of reaction
2. First order reaction: The reaction in which the rate of R x n depends only on one concentration is doubled. Rate of reaction will also be doubled.
Equations: A → Products
t = 0 a mole/lit 0
t = t a – x x
Rate = K [A]¹
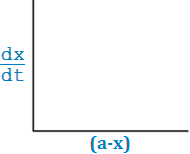
Rate = – dCR/dt = d [A]/dt = + K [A]
– d (a – x)/ dt = – K (a – x)
dx/ dt = K (a – x)
∫dx/ (a – x) = ∫ Kdt
– log (a – x) = Kt + c
When t = 0, x = 0
– log a = c
– log (a – x) = Kt – log a
Kt = 2030 log (a/a – x)
a = is initial concentration
x = is dissociated concentration.
log (a – x) = – Kt/2.303 + log a
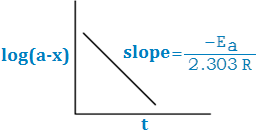
And also
m (a/a-x) = Kt
a/(a – x) = eKt ⇒ (a – x)/a = e¯Kt
x = a (1 – e¯Kt)
Half-life of first order Reaction:
log (a/a-x) = Kt/2.303
t = 2.303/K log (a/a-x)
t = t½ ⇒ x = a/2
K = (2.303/ t½) log2 = 0.693/ t½
t½ = 0.693/K [It is independent of initial concentration]
For the first order reaction.
\(M\xrightarrow{1{{t}_{1/2}}}\frac{M}{2}\xrightarrow{2{{t}_{1/2}}}\frac{M}{4}\xrightarrow{3{{t}_{1/2}}}\frac{M}{8}\)Amount of reaction left after time t = Initial Amount/ 2ⁿ
η = t/t½ = Number of half – lifes
3. nth Order Reaction: A → Products
Rate law is (dn/dt) = K [A]ⁿ = K (a – x)ⁿ
\({{K}_{\eta }}=\frac{1}{\left( n-1 \right)t}\left[ \frac{1}{{{\left( a-x \right)}^{n-1}}}-\frac{1}{{{a}^{n-1}}} \right]\)Time T is required to complete a particular fraction of reaction.
T α (a)¹¯ⁿ
If concentration is changed m times new rate will be mⁿ
Half-life of nth order reaction:
t½ α 1/aⁿ¯¹
a is initial concentration
η is order of Reaction
Half-life of nth order reaction
\(t\frac{1}{2}=\frac{{{2}^{n-1}}-1}{K\left( n-1 \right){{a}^{n-1}}}\)\(\frac{{{\left( t\frac{1}{2} \right)}_{1}}}{{{\left( t\frac{1}{2} \right)}_{2}}}={{\left( \frac{{{a}_{2}}}{{{a}_{1}}} \right)}^{n-1}}\)
| Reaction Order | Differential Rate Law | Integrated Rate Law | Characteristics Kinetic Plot | Slope of Kinetic Plot |
Units of Rate Constant |
| Zero | – d[A]/dt = K | [A] = [A]₀ – Kt | [A] vs t | – K |
Mole L¯¹ sec¯¹ |
|
First |
– d[A]/dt = K[A] | [A] = [A]₀ e-Kt | ln [A] vs t | – K | sec¯¹ |
| Second | – d[A]/dt = K[A]² | [A] = [A]₀/1 + Kt[A]₀ | 1/[A] vs t |
K |
L Mole sec¯¹ |
