Impulse

Impulse

1) When a large force works on a body for every small time interval, it is called as impulsive force. An impulsive force does not remain constant, but changes first from zero to maximum and then from maximum to zero. In such case we measure the total effect of force.

2) Impulsive of a force is a measure of total effect of force.

3) \(\overrightarrow{I}=\int\limits_{{{t}_{1}}}^{{{t}_{2}}}{\overrightarrow{F}.dt}\)

4) Impulsive is a vector quantity and its direction is same as that of force.

5) Dimension: \(\left[ ML{{T}^{-}} \right]\)

6) Units: Newton – Second (or) \(kg.m/\sec \)

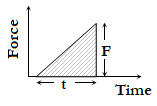
7) Force – Time Graph: Impulsive is equal to the area under F – t curve. If we plot a graph between force and time, they are under the curve and time axis gives the value of impulse.

\(I=\) Area between curve and time axis = \(\frac{1}{2}\times Base\times Height=\frac{1}{2}Ft\)

8) If \({{F}_{avg}}\) is the average magnitude of the force then, \(I=\int\limits_{{{t}_{1}}}^{{{t}_{2}}}{Fdt}={{F}_{avg}}\int\limits_{{{t}_{1}}}^{{{t}_{2}}}{dt}={{F}_{avg}}\Delta t\)

9) From Newton’s second law: \(\overrightarrow{F}=\frac{d\overrightarrow{p}}{dt}\),\(\Rightarrow \int\limits_{{{t}_{1}}}^{{{t}_{2}}}{\overrightarrow{F}dt}=\int\limits_{{{p}_{1}}}^{{{p}_{2}}}{d\overrightarrow{p}}\)\(\Rightarrow \overrightarrow{I}=\overrightarrow{{{p}_{2}}}-\overrightarrow{{{p}_{1}}}=\overrightarrow{\Delta p}\)

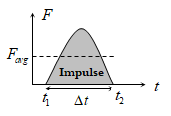
i.e. The momentum of a force is equal to the change in momentum. This statement is known as Impulse momentum theorem. Examples: Kicking, catching, jumping, diving, collision etc.

In all these cases an impulse acts. \(I=\int{Fdt={{F}_{avg}}.\Delta t}=\Delta p\) = constant.

So, if time of contact \(\Delta t\) is increased, average force is decreased and vice – versa.