Hyperbola – Position of a Point with respect to a Hyperbola and Conjugate

Hyperbola – Position of a Point with respect to a Hyperbola and Conjugate

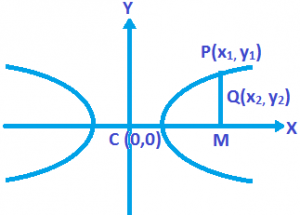
Position of a Point with respect to a Hyperbola: The quantity  \(\frac{{{x}_{1}}^{2}}{{{a}^{2}}}-\frac{{{y}_{1}}^{2}}{{{b}^{2}}}-1\) is positive zero (or) negative according as the point (x₁, y₁) lies within, upon or outside the curve, respectively.

If (x₁, y₁) lies on the hyperbola.

Then

\(\frac{{{x}_{1}}^{2}}{{{a}^{2}}}-\frac{{{y}_{1}}^{2}}{{{b}^{2}}}-1=0\).

\(\left( \frac{{{x}_{1}}^{2}}{{{a}^{2}}}-1 \right){{b}^{2}}\) = y₁².

Now if P lies outside the curve then

y₁² > y₂²

y₁² > \(\left( \frac{{{x}_{1}}^{2}}{{{a}^{2}}}-1 \right){{b}^{2}}\).

\(\frac{{{x}_{1}}^{2}}{{{a}^{2}}}-\frac{{{y}_{1}}^{2}}{{{b}^{2}}}-1<0\).

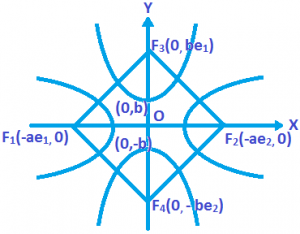
Conjugate Hyperbola: Corresponding to every hyperbola, there exists a hyperbola such that the conjugate axis of one is equal to the transverse axis and conjugate axis of the other. Such hyperbolas are known as conjugate to each other.

Hence for the hyperbola

\(\frac{{{x}_{1}}^{2}}{{{a}^{2}}}-\frac{{{y}_{1}}^{2}}{{{b}^{2}}}=1\).

The Conjugate hyperbola is \(\frac{{{x}_{1}}^{2}}{{{a}^{2}}}-\frac{{{y}_{1}}^{2}}{{{b}^{2}}}=-1\).