Potential energy is the ability of an object to store energy based on its position. For example, if you stretch a rubber band, to the farthest point energy will be stored in the object based on its position. The same thing happens when a wrecking ball is used to demolish buildings.
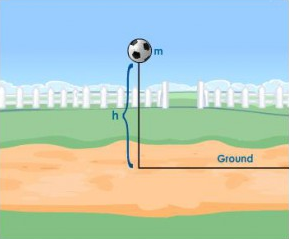
The definition for gravitational potential energy is as such, “The energy stored in an object based on its position in the gravitational field”. It is dependent on the weight of the object and the height of the body displaced from position zero. Position zero is commonly taken as the surface of the earth, but can be redefined for experimental purposes.
The work done in moving a unit mass from infinity to a point in a gravitational field is called the Gravitational Potential at that point. It is a negative, Scalar quantity, the units is Jkg-1.
Derivation of Gravitational Potential Energy: Let a body of mass m be at a distance r from a body of mass M. the gravitational potential energy of the mass m is defined as the work done in bringing it from infinity to that point.
We know,
\(F\,=\,\frac{GMm}{{{r}^{2}}}\)
Where, F is the force between M and m.
The work done in moving the mass m through a small distance in the gravitational field of M is,
dW = F.dr
\(dW\,=\,\frac{GMm}{{{r}^{2}}}.dr\)
The total work done in bringing mass m from infinity to that point is,
\(\int{dW}\,=\,\int\limits_{\infty }^{r}{\frac{GMm}{{{r}^{2}}}}.dr\,=\,-\,\int\limits_{r}^{\infty }{\frac{GMm}{{{r}^{2}}}}.dr\)
\(W\,=\,-\,GMm\,\int\limits_{r}^{\infty }{\frac{dr}{{{r}^{2}}}}\)
= \(-\,GMm\,\,\left[ \frac{-1}{r} \right]_{r}^{\infty }\),
= \(-\,GMm\,\left[ 0\,\,-\,\,\left( -\frac{1}{r} \right) \right]\) ,
= \(-\,GMm\left[ \frac{+1}{r} \right]\)
= \(-\,\frac{GMm}{r}\)
Therefore,
Gravitational Potential Energy = \(-\,\frac{GMm}{r}\).
How to find the Gravitational Potential Energy?
Example: What is the Gravitational Potential Energy of the moon with respect to the earth? The mass of the moon is 7.35 x 10²² kg and the mass of the earth is5.98 x 10²⁴ kg. The earth moon distance is 384400km.
Solution: We know that,
Gravitational Constant (G) = 6.67 x 10¯¹¹ m³/kg.sec²
Mass of the moon (M) = 7.35 x 10²² kg
Mass of the earth (m) = 5.98 x 10²⁴ kg
Distance(r) = 384400 km
Now,
Gravitational Potential Energy = \(-\,\,\frac{GMm}{r}\)
= \(-\,\,\frac{6.67\times {{10}^{-11}}\times 7.35\times {{10}^{22}}\times 5.98\times {{10}^{24}}}{384400\times {{10}^{3}}}\)
= – 7.63 x 10²⁸ Joules.
