Gravitational Filed:
The space surrounding a material body in which its gravitational force of attraction can be experienced is called its gravitational field.
Gravitational Filed Intensity:
Gravitational filed intensity at any point is defined as the gravitational force experienced by any test mass divided by the magnitude of test mass when placed at desired point.
E = Fr /mₒ
It means that the mass is so small it doesn’t effect the original filed when brought there.
E is the vector quantity and its direction is same as that of Fr it is expressed in Nkg-1
Gravitational Filed Intensity due to various Mass Distributions:
1. Due to point mass, the gravitational filed intensity at p distance r form the point mass m, is given by E = Gm/r² it is directed towards the point mass.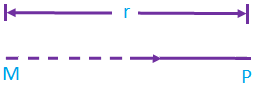
2. Due to ring having a uniform mass distribution.
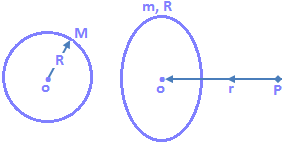At the centre E = 0On the axis E = [Gmr/ (R² + r²)³/²] PO
3. Due to hollow sphere having a uniform mass distribution. For inside point, (r < R) E = 0. For outside point, (r ≥ R) E = GM/r²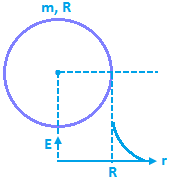
Where r is the distance of point form the centre.
So, form the above expression, we can say gravitational filed intensity due to hollow sphere having uniform mass distribution at any outside point is same as if the entire mass is concentrate at its centre.
4. Due to solid sphere having a uniform mass distribution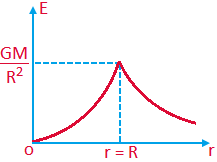
For inside point (r < R)
E = Gmr/ R³
For outside point (r ≥ R)
E = – Gm/r²
Example: Infinite no. of bodies, each of mass 3kg are situated at distances 1m, 2m, 4m, 8m. Respectively on x-axis. The resultant intensity of gravitational field at the origin will be
(A) G (B) 2G (C) 3G (D) 4G
Solution: Intensity at the origin
= GM/r₁² + GM/r₂² + GM/r₃² + GM/r₄² + ….
= GM [1 + ¼ + 1/16 + 1/ 64 + …]
= GM [1/ (1 – ¼)]
= GM x 4/3 = G x 3 x 4/3 = 4G
Example: Knowing that mass of Moon is M/81 where M is the mass of Earth, find the distance of the point where gravitational field due to Earth and Moon cancel each other, from the Moon. Given that distance between Earth and Moon is 60 R. Where R is the radius of Earth
(a) 2R (b) 4R (c) 6R (d) 8R
Solution: Point of zero intensity X = √m₁ d/ (√m₁ + √m₂)
Mass of the earth m₁, Mass of the moon m₂ = M/81
And distance between earth & moon d = 60 R
Point of zero intensity from the Earth X = √M x 60 R / (√M + √M/81) = 54